基于硬约束物理信息神经网络的含水层渗透系数场反演

doi:10.13745/j.esf.sf.2025.10.38

摘要/Abstract

摘要：

近年来,物理信息神经网络(physics-informed neural networks,PINNs)在数值求解偏微分方程和计算流体力学等领域得到了广泛应用,并在地下水模拟中展现出初步的应用潜力。现有研究中,PINNs对地下水模型边界条件的处理通常采用软约束算法,通过边界条件误差最小化来近似满足物理约束。然而,能够进一步提升求解精度和稳定性的硬约束算法在该领域的应用仍较为有限。为此,本文引入PINNs硬约束方法,提出了一种同时考虑定水头边界和隔水边界条件的PINNs硬约束算法,并以二维承压含水层的渗透系数场反演为例,对比分析了硬约束PINNs相较于软约束PINNs在提高渗透系数场反演精度方面的优势。结果表明,所提出的硬约束PINNs方法的反演平均相对误差相比软约束PINNs降低了75%,且相较于仅考虑定水头边界的硬约束PINNs反演平均相对误差减少了60%。此外,该方法能够有效减少训练所需样本数量和超参数数量,降低人为因素对模型训练的影响,提升了训练效率。因此,该硬约束PINNs方法在含水层渗透系数场反演中展现出良好的精度与效率,具有良好的推广应用前景。

关键词: 物理信息神经网络, 硬约束PINNs, 渗透系数场反演, 地下水建模, 承压含水层

Abstract:

In recent years, Physics-Informed Neural Networks (PINNs) have been widely applied to numerically solve partial differential equations and in computational fluid dynamics, having demonstrated promising potential for groundwater modeling. Existing studies typically handle boundary conditions in groundwater models using soft-constraint algorithms, which satisfy physical constraints approximately by minimizing the boundary condition error. However, the application of hard-constraint algorithms, which can enhance solving accuracy and stability by design, remains limited in groundwater modeling. To address this gap, this paper introduces a hard-constraint PINNs algorithm that simultaneously enforces constant-head and no-flow boundary conditions. Using the inverse problem of estimating the hydraulic conductivity field in a two-dimensional confined aquifer as a case study, we demonstrate the superior performance of the hard-constraint approach over its soft-constraint counterpart. The results show that the proposed method reduces the average relative inversion error by 75% compared to soft-constraint PINNs and by 60% compared to hard-constraint PINNs considering constant-head boundaries alone. Furthermore, the proposed method reduces the number of required training samples and alleviates the need for extensive manual hyperparameter tuning, thereby improving training efficiency and robustness. Therefore, the hard-constraint PINNs method proves to be a highly accurate and efficient approach for reconstructing hydraulic conductivity fields, demonstrating significant potential for broader application.

Key words: physics-informed neural networks, hard-constraint PINNs, hydraulic conductivity field inversion, groundwater modeling, confined aquifer

中图分类号:

P641.2

舒伟, 蒋建国, 吴吉春. 基于硬约束物理信息神经网络的含水层渗透系数场反演[J]. 地学前缘, 2026, 33(1): 500-510.

SHU Wei, JIANG Jianguo, WU Jichun. Physics-informed neural networks with hard constraints for hydraulic conductivity field inversion[J]. Earth Science Frontiers, 2026, 33(1): 500-510.

图/表 8

图1 PINNs网络结构及求解偏微分方程示意图

Fig.1 Schematic diagram of the PINNs architecture and the solution process for partial differential equations

图2 PINNs软约束算法与硬约束算法示意图

Fig.2 Schematic diagram of the soft-constraint and hard-constraint PINNs algorithms

图3 研究区概况图

Fig.3 Schematic diagram of the study area

图4 PINNs硬约束算法反演渗透系数场原理图

Fig.4 Schematic diagram of the PINNs hard-constraint algorithm for permeability field inversion

表1 二维承压水流模型PINNs算例所采用的计算超参数

Table 1 Computational hyperparameters used in the PINNs examples for the two-dimensional confined groundwater flow model

PINNs算法	N_f	N_B	N_D	NN₁	NN₂/NN₃	NN_K
PINNs-S	400	200	25	100×6		60×6
PINNs-H-I	400	200	25	100×6		60×6
PINNs-H-II	400	200	25	100×6	100×3	60×6
PINNs-H-III	400		25	100×6	100×3	60×6

图5 各PINNs算法在二维承压含水层K场反演中的结果对比第一列为参考K场;第二列为不同PINNs算法反演的K场;第三列为反演K场与参考K场的绝对误差。

Fig.5 Comparison of the inversion results of different PINNs algorithms for the K field in a two-dimensional confined aquifer

图6 4种PINNs算法反演K场的4种模型性能评价指标图

Fig.6 Model performance evaluation metrics of the K field inverted by four different PINNs algorithms

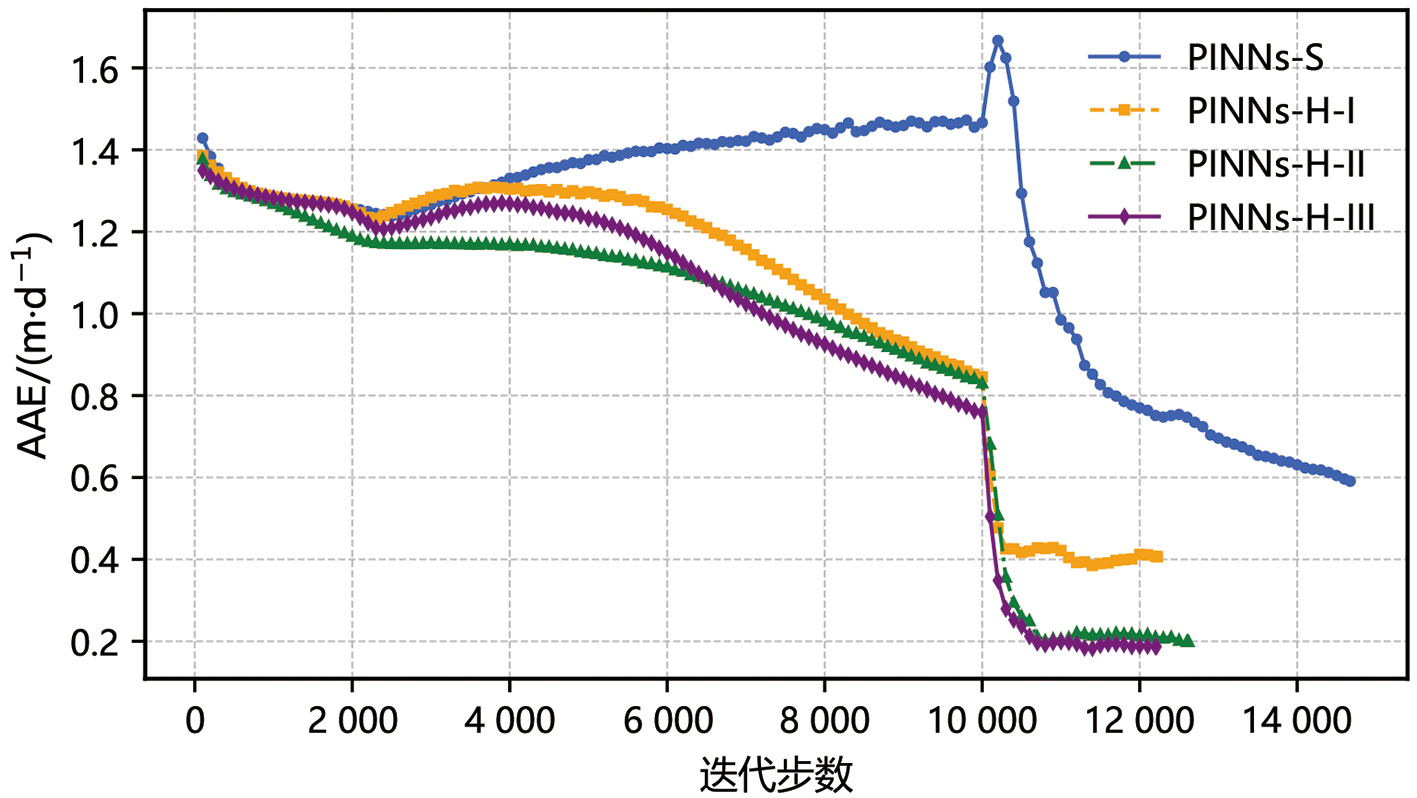
图7 4种PINNs算法反演K场与参考K场的AAE随迭代步数的变化情况图

Fig.7 Variation of the average absolute error (AAE) between the inverted and reference K fields with the number of training iterations for the four PINNs algorithms

参考文献 41

[1]	RAISSI M, PERDIKARIS P, KARNIADAKIS G E. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378: 686-707. DOI URL
[2]	RAISSI M, YAZDANI A, KARNIADAKIS G E. Hidden fluid mechanics: learning velocity and pressure fields from flow visualizations[J]. Science, 2020, 367(6481): 1026-1030. DOI PMID
[3]	SUN L N, GAO H, PAN S W, et al. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 361: 112732. DOI URL
[4]	MATHEWS A, FRANCISQUEZ M, HUGHES J W, et al. Uncovering turbulent plasma dynamics via deep learning from partial observations[J]. Physical Review E, 2021, 104(2): 025205. DOI URL
[5]	PANG G, D’ELIA M, PARKS M, et al. nPINNs: nonlocal physics-informed neural networks for a parametrized nonlocal universal Laplacian operator. Algorithms and applications[J]. Journal of Computational Physics, 2020, 422: 109760. DOI URL
[6]	MENG X H, LI Z, ZHANG D K, et al. PPINN: parareal physics-informed neural network for time-dependent PDEs[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 370: 113250. DOI URL
[7]	JAGTAP A D, KHARAZMI E, KARNIADAKIS G E. Conservative physics-informed neural networks on discrete domains for conservation laws: applications to forward and inverse problems[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 365: 113028. DOI URL
[8]	YANG L, MENG X H, KARNIADAKIS G E. B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data[J]. Journal of Computational Physics, 2021, 425: 109913. DOI URL
[9]	ZHANG X P, ZHU Y, WANG J, et al. GW-PINN: a deep learning algorithm for solving groundwater flow equations[J]. Advances in Water Resources, 2022, 165: 104243. DOI URL
[10]	GUO H W, ZHUANG X Y, CHEN P W, et al. Stochastic deep collocation method based on neural architecture search and transfer learning for heterogeneous porous media[J]. Engineering with Computers, 2022, 38(6): 5173-5198. DOI
[11]	DONG S C, NI N X. A method for representing periodic functions and enforcing exactly periodic boundary conditions with deep neural networks[J]. Journal of Computational Physics, 2021, 435: 110242. DOI URL
[12]	WANG S F, TENG Y J, PERDIKARIS P. Understanding and mitigating gradient flow pathologies in physics-informed neural networks[J]. SIAM Journal on Scientific Computing, 2021, 43(5): A3055-A3081.
[13]	CHEN J R, DU R, WU K K. A comparison study of deep Galerkin method and deep ritz method for elliptic problems with different boundary conditions[J]. Communications in Mathematical Research, 2020, 36(3): 354-376. DOI URL
[14]	ZEINHOFER M, MASRI R, MARDAL K A. A unified framework for the error analysis of physics-informed neural networks[J]. IMA Journal of Numerical Analysis, 2025, 45(5): 2988-3025. DOI URL
[15]	BERRONE S, CANUTO C, PINTORE M, et al. Enforcing Dirichlet boundary conditions in physics-informed neural networks and variational physics-informed neural networks[J]. Heliyon, 2023, 9(8): e18820. DOI URL
[16]	LEAKE C, MORTARI D. Deep theory of functional connections: a new method for estimating the solutions of partial differential equations[J]. Machine Learning and Knowledge Extraction, 2020, 2(1): 37-55. DOI PMID
[17]	SUKUMAR N, SRIVASTAVA A. Exact imposition of boundary conditions with distance functions in physics-informed deep neural networks[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 389: 114333. DOI URL
[18]	WANG S F, SANKARAN S, PERDIKARIS P. Respecting causality for training physics-informed neural networks[J]. Computer Methods in Applied Mechanics and Engineering, 2024, 421: 116813. DOI URL
[19]	LU L, PESTOURIE R, YAO W J, et al. Physics-informed neural networks with hard constraints for inverse design[J]. SIAM Journal on Scientific Computing, 2021, 43(6): B1105-B1132.
[20]	BARSCHKIS S. Exact and soft boundary conditions in physics-informed neural networks for the variable coefficient Poisson equation[J]. arXiv preprint arXiv:2310.02548, 2023.
[21]	TOSCANO J D, KÄUFER T, MAXEY M, et al. Inferring turbulent velocity and temperature fields and their statistics from Lagrangian velocity measurements using physics-informed Kolmogorov-Arnold Networks[J]. arXiv preprint arXiv:2407.15727, 2024.
[22]	ANAGNOSTOPOULOS S J, TOSCANO J D, STERGIOPULOS N, et al. Learning in PINNs: phase transition, diffusion equilibrium, and generalization[J]. Neural Networks, 2026, 193: 107983. DOI URL
[23]	JIN P Z, ZHANG Z, ZHU A Q, et al. SympNets: intrinsic structure-preserving symplectic networks for identifying Hamiltonian systems[J]. Neural Networks, 2020, 132: 166-179. DOI PMID
[24]	ZHOU K, GRAUER S J. Flow reconstruction and particle characterization from inertial Lagrangian tracks[J]. arXiv preprint arXiv:2311.09076, 2023.
[25]	WANG N Z, CHANG H B, ZHANG D X. Efficient uncertainty quantification for dynamic subsurface flow with surrogate by theory-guided neural network[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 373: 113492. DOI URL
[26]	JIN X W, CAI S Z, LI H, et al. NSFnets (Navier-Stokes flow nets): physics-informed neural networks for the incompressible Navier-Stokes equations[J]. Journal of Computational Physics, 2021, 426: 109951. DOI URL
[27]	CUOMO S, DI COLA V S, GIAMPAOLO F, et al. Scientific machine learning through physics-informed neural networks: where we are and what’s next[J]. Journal of Scientific Computing, 2022, 92(3): 88. DOI
[28]	邓书超, 宋孝天, 钟旻霄, 等. 一种求解偏微分方程的动态平衡物理信息神经网络[J]. 中国科学: 信息科学, 2024, 54(3): 18431859.
[29]	TIAN Y J, ZHANG Y Q, ZHANG H B. Recent advances in stochastic gradient descent in deep learning[J]. Mathematics, 2023, 11(3): 682. DOI URL
[30]	BAYDIN A G, PEARLMUTTER B A, RADUL A A, et al. Automatic differentiation in machine learning: a survey[J]. Journal of Machine Learning Research, 2018, 18(1): 5595-5637.
[31]	ABADI M, BARHAM P, CHEN J, et al. TensorFlow:A system for large-scale machine learning[C]//Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI’16). Savannah, GA, USA: USENIX Association, 2016: 265-283.
[32]	PASZKE A, GROSS S, CHINTALA S, et al. Automatic differentiation in PyTorch[C]. The NIPS 2017 Autodiff Workshop. Long Beach, CA, USA: Neural Information Processing Systems Foundation, 2017.
[33]	NANNI L, LUMINI A, GHIDONI S, et al. Stochastic selection of activation layers for convolutional neural networks[J]. Sensors, 2020, 20(6): 1626. DOI URL
[34]	MENG X H, YAN J Y, YE H L, et al. Construction and approximation for a class of feedforward neural networks with sigmoidal function[J]. International Journal of Wavelets, Multiresolution and Information Processing, 2023, 21(6): 2350028. DOI URL
[35]	GODIN F, DEGRAVE J, DAMBRE J, et al. Dual rectified linear units (DReLUs): a replacement for tanh activation functions in quasi-recurrent neural networks[J]. Pattern Recognition Letters, 2018, 116: 8-14. DOI URL
[36]	VENKATESWARARAO P, MURUGAVALLI S. Rectifying the problem of vanishing gradient using ReLU activation function based on BLSTM neural network[J]. International Journal of Recent Technology and Engineering, 2019, 8(1): 2615-2618.
[37]	MAAS A L, HANNUN A Y, NG A Y. Rectifier nonlinearities improve neural network acoustic models[C]// Proceedings of the 30th International Conference on Machine Learning. Atlanta, GA, USA: JMLR: W&CP, 2013: 1-9.
[38]	RAMACHANDRAN P, ZOPH B, LE Q V. Searching for activation functions[J]. arXiv preprint arXiv:1710.05941, 2017.
[39]	ALZUBAIDI L, ZHANG J L, HUMAIDI A J, et al. Review of deep learning: concepts, CNN architectures, challenges, applications, future directions[J]. Journal of Big Data, 2021, 8(1): 53. DOI PMID
[40]	WANG Q, MA Y, ZHAO K, et al. A comprehensive survey of loss functions in machine learning[J]. Annals of Data Science, 2022, 9(2): 187-212. DOI
[41]	ALIAKBARI M, SOLTANY SADRABADI M, VADASZ P, et al. Ensemble physics informed neural networks: a framework to improve inverse transport modeling in heterogeneous domains[J]. Physics of Fluids, 2023, 35(5): 053616. DOI URL