

地学前缘 ›› 2026, Vol. 33 ›› Issue (1): 313-327.DOI: 10.13745/j.esf.sf.2025.10.29
许林1,2( ), 马海春2, 王京平2, 张庆3, 黄逸航2, 钱家忠2,*(
), 马海春2, 王京平2, 张庆3, 黄逸航2, 钱家忠2,*( ), 王万林2,4
), 王万林2,4
收稿日期:2025-08-10
修回日期:2025-10-16
出版日期:2026-01-25
发布日期:2025-11-10
通信作者:
*钱家忠(1968—),男,博士,教授,博士生导师,主要从事地下水污染与防治教学和科研工作。E-mail: qianjiazhong@hfut.edu.cn
作者简介:许 林(1993—),男,硕士,主要从事污染土壤/地下水修复、矿山生态修复等相关研究工作。E-mail: 251216902@qq.com
基金资助:
XU Lin1,2( ), MA Haichun2, WANG Jingping2, ZHANG Qing3, HUANG Yihang2, QIAN Jiazhong2,*(
), MA Haichun2, WANG Jingping2, ZHANG Qing3, HUANG Yihang2, QIAN Jiazhong2,*( ), WANG Wanlin2,4
), WANG Wanlin2,4
Received:2025-08-10
Revised:2025-10-16
Online:2026-01-25
Published:2025-11-10
摘要:
随着深部资源勘探、地热能源开发和核废料地质处置等工程活动的深入推进,地下水在高地应力高温环境下的渗流行为成为研究热点,进而关于如何构建适用于高地应力高温条件的多物理场耦合理论模型,以准确反映在真实地应力和温度条件下水-岩相互作用、裂隙形态演化与流体特性变化的动态过程成为重点关注的问题。本文系统综述了高地应力高温条件下地下水渗流的基本理论、实验研究与数值模拟进展,重点阐述了传统立方定律在裂隙渗流模拟中的适用性与局限,并介绍了非达西流与广义达西流的理论拓展,分析了地应力与温度对渗透率的耦合调控机制;总结了多项地应力与热力耦合实验成果及其渗流参数演化规律,探讨了数值模拟中地应力主导下裂隙几何形态演变与渗透通道演化过程;评价了高温环境下矿物热膨胀、热破裂与裂隙粗糙度变化对渗流路径的影响,评估了热-水-力耦合模型及数据驱动方法的预测潜力;评述了当前理论模型在高地应力高温多场耦合机制、裂隙尺度效应及长期演化方面仍存在不足,展望了未来的研究方向。
中图分类号:
许林, 马海春, 王京平, 张庆, 黄逸航, 钱家忠, 王万林. 高地应力高温条件裂隙介质地下水非线性渗流研究进展[J]. 地学前缘, 2026, 33(1): 313-327.
XU Lin, MA Haichun, WANG Jingping, ZHANG Qing, HUANG Yihang, QIAN Jiazhong, WANG Wanlin. Advances in groundwater nonlinear seepage in fractured media under conditions of high in-situ stress and temperature[J]. Earth Science Frontiers, 2026, 33(1): 313-327.
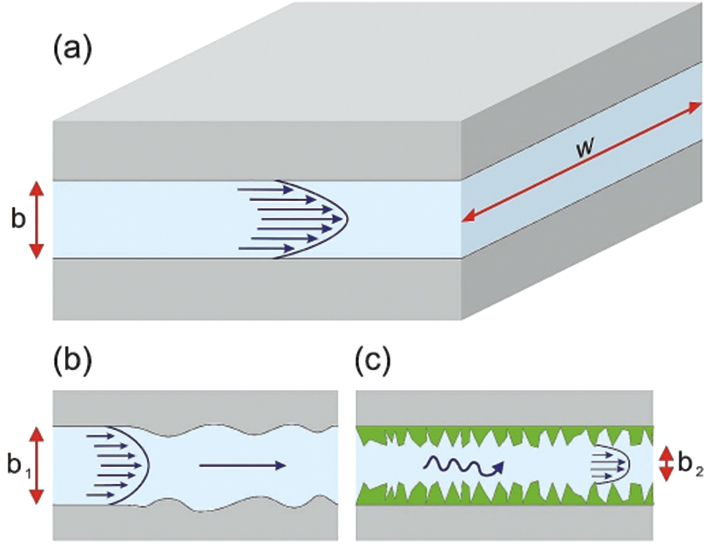
图1 裂隙中地下水流动示意图(据文献[24]) a—光滑平行裂隙中地下水(蓝色)流动,灰色为岩体基质;b—非平行裂隙中地下水流动;c—粗糙裂隙中地下水流动,绿色为局部“凸起”。
Fig.1 Schematic diagram of groundwater flow in fractures. Adapted from [24].
| 方程的类型 | 方程 | 提出的学者 | 术语解释 | 评论 |
|---|---|---|---|---|
| 多项式方程 | i=aq+bq2 | Forchheimer[ | a和b为常数 | 经验性,但理论基础 是后来才找到的 |
| i=aq+bq2+cq3 | Forchheimer[ | a、b和c为常数 | 经验性 | |
| i=aq+bq1.5+cq2 | Rose[ | a、b和c为常数 | 经验性 | |
| i=aq+bq2+c(∂v/∂t) | Polubarinova-Kochina[ | a、b和c为常数 | 经验性 | |
| i=aq+bqm | Muskat[ Harr[ | a、b和m为常数 | 经验性 | |
| 幂律方程 | q=Min, n<1 | Izbash[ | M和n为常数 | 经验值n介于1和0.5之间 |
| q=(Bi)1/2 | Escande[ | B为常数 | 对于直径为2.54 cm的 颗粒,经验系数B在80至 290(cm/s)2之间变化。 | |
| q=32.9m1/2i0.54 | Wilkins[ | m为水力开度 | 基于1.905~7.62 cm颗粒 测试结果的半经验方法 | |
| q=α(μ/σ)f-1(ki)f | Slepicka[ | α、f和k为常数; μ表示黏度; σ表示表面张力 | 半经验的,由维数分析得出 | |
| q=n(igd/Kst)1/2 | Stephenson[ | d为颗粒直径;n为孔隙率; g为重力常数; Kst为斯蒂芬森摩擦因数 | 半经验性的,更适合 在场地尺度上使用 |
表1 高雷诺数下已发表的非达西定律
Table 1 Published non-Darcian flow laws at the high Reynolds’s numbers
| 方程的类型 | 方程 | 提出的学者 | 术语解释 | 评论 |
|---|---|---|---|---|
| 多项式方程 | i=aq+bq2 | Forchheimer[ | a和b为常数 | 经验性,但理论基础 是后来才找到的 |
| i=aq+bq2+cq3 | Forchheimer[ | a、b和c为常数 | 经验性 | |
| i=aq+bq1.5+cq2 | Rose[ | a、b和c为常数 | 经验性 | |
| i=aq+bq2+c(∂v/∂t) | Polubarinova-Kochina[ | a、b和c为常数 | 经验性 | |
| i=aq+bqm | Muskat[ Harr[ | a、b和m为常数 | 经验性 | |
| 幂律方程 | q=Min, n<1 | Izbash[ | M和n为常数 | 经验值n介于1和0.5之间 |
| q=(Bi)1/2 | Escande[ | B为常数 | 对于直径为2.54 cm的 颗粒,经验系数B在80至 290(cm/s)2之间变化。 | |
| q=32.9m1/2i0.54 | Wilkins[ | m为水力开度 | 基于1.905~7.62 cm颗粒 测试结果的半经验方法 | |
| q=α(μ/σ)f-1(ki)f | Slepicka[ | α、f和k为常数; μ表示黏度; σ表示表面张力 | 半经验的,由维数分析得出 | |
| q=n(igd/Kst)1/2 | Stephenson[ | d为颗粒直径;n为孔隙率; g为重力常数; Kst为斯蒂芬森摩擦因数 | 半经验性的,更适合 在场地尺度上使用 |
| 研究学者 | 研究内容 | 实验方法 | 主要结论 |
|---|---|---|---|
| 王恩志等[ | 研究地应力作用下低渗透砂岩的稳定渗流特性,以盐水为渗流介质,探讨渗透性与有效地应力的关系 | 采用恒速法和恒压法,进行低渗透饱和砂岩在不同地应力条件下的渗流实验 | 岩石渗透率随有效地应力增加而显著下降,呈现非线性变化关系,说明地应力对渗流能力具有显著抑制作用 |
| 徐德敏等[ | 对大尺寸低渗透软弱岩进行高地应力渗流试验,进一步分析地应力变化对渗透性的影响 | 利用自主研制的高地应力渗流仪开展系统性试验,监测渗透系数随地应力变化的动态响应 | 渗透系数随地应力增加而降低,且在地应力卸载时虽有回升,但未恢复至初始水平;认为渗透性变化主要源于侧向压力导致孔隙和喉道的压缩变形 |
| 蒋宇静等[ | 探讨含原岩充填物的砂岩裂隙在不同轴压和地应力下的渗流响应 | 在轴压0.01~0.2 MPa、地应力0~10 MPa条件下,开展充填裂隙渗流实验,比较不同粒度填充物和裂隙开度的影响 | 对充填裂隙岩体,地应力显著影响渗流能力;开度较大的无充填裂隙中,地应力影响甚微。轴压<0.03 MPa或地应力<1 MPa时,粒度影响无序;当轴压与地应力较高时,粒径越大,渗流量越大 |
| 王俊光和梁冰[ | 针对高地应力、高水压条件下含充填裂隙岩体的渗透性特征开展实验研究 | 采用自主研发的三轴应力-渗流耦合试验系统,对不同充填材料裂隙试样进行渗透性测试 | 不同充填物裂隙样品的渗透系数存在差异,但在相同地应力下数量级相近;渗透系数随地应力增大而持续下降,体现出地应力对裂隙渗透性能的压缩效应 |
| 刘杰等[ | 探讨高水压环境中裂隙渗流能力的变化规律,强调应力与渗流之间的耦合关系 | 开展野外原位渗流实验,模拟地下高水压环境,分析地应力对裂隙导水能力的约束作用 | 研究表明高水压增强裂隙导水能力,但地应力则对其具有显著抑制作用;裂隙渗流引发应力变化,同时应力反过来也影响渗透性,显示出渗流-应力间的强耦合特性 |
| 刘欣语[ | 评估渗透水压对岩石力学特性和渗透性的影响,强调耦合分析的重要性 | 利用数值与理论分析方法,讨论地下水压力对岩体强度与渗透演化的联动机制 | 认为单一考虑水压力不足以解释实际渗流现象,应从渗流-应力耦合视角开展系统研究,以更全面理解地下水活动及其对岩体结构的影响 |
| 左宇军等[ | 研究不同渗透压差与地应力条件下,页岩试样的渗透性演化过程 | 采用应力-应变控制渗透性试验,测定不同压力组合下的渗透系数变化 | 在相同渗透压差条件下,渗透率随地应力增大而降低;在相同地应力下,渗透率随渗透压差增大而升高,说明渗透驱动力和地应力共同调控裂隙渗流行为 |
表2 地应力耦合地下水渗流的实验研究
Table 2 Experimental study on confining pressure coupled with groundwater seepage
| 研究学者 | 研究内容 | 实验方法 | 主要结论 |
|---|---|---|---|
| 王恩志等[ | 研究地应力作用下低渗透砂岩的稳定渗流特性,以盐水为渗流介质,探讨渗透性与有效地应力的关系 | 采用恒速法和恒压法,进行低渗透饱和砂岩在不同地应力条件下的渗流实验 | 岩石渗透率随有效地应力增加而显著下降,呈现非线性变化关系,说明地应力对渗流能力具有显著抑制作用 |
| 徐德敏等[ | 对大尺寸低渗透软弱岩进行高地应力渗流试验,进一步分析地应力变化对渗透性的影响 | 利用自主研制的高地应力渗流仪开展系统性试验,监测渗透系数随地应力变化的动态响应 | 渗透系数随地应力增加而降低,且在地应力卸载时虽有回升,但未恢复至初始水平;认为渗透性变化主要源于侧向压力导致孔隙和喉道的压缩变形 |
| 蒋宇静等[ | 探讨含原岩充填物的砂岩裂隙在不同轴压和地应力下的渗流响应 | 在轴压0.01~0.2 MPa、地应力0~10 MPa条件下,开展充填裂隙渗流实验,比较不同粒度填充物和裂隙开度的影响 | 对充填裂隙岩体,地应力显著影响渗流能力;开度较大的无充填裂隙中,地应力影响甚微。轴压<0.03 MPa或地应力<1 MPa时,粒度影响无序;当轴压与地应力较高时,粒径越大,渗流量越大 |
| 王俊光和梁冰[ | 针对高地应力、高水压条件下含充填裂隙岩体的渗透性特征开展实验研究 | 采用自主研发的三轴应力-渗流耦合试验系统,对不同充填材料裂隙试样进行渗透性测试 | 不同充填物裂隙样品的渗透系数存在差异,但在相同地应力下数量级相近;渗透系数随地应力增大而持续下降,体现出地应力对裂隙渗透性能的压缩效应 |
| 刘杰等[ | 探讨高水压环境中裂隙渗流能力的变化规律,强调应力与渗流之间的耦合关系 | 开展野外原位渗流实验,模拟地下高水压环境,分析地应力对裂隙导水能力的约束作用 | 研究表明高水压增强裂隙导水能力,但地应力则对其具有显著抑制作用;裂隙渗流引发应力变化,同时应力反过来也影响渗透性,显示出渗流-应力间的强耦合特性 |
| 刘欣语[ | 评估渗透水压对岩石力学特性和渗透性的影响,强调耦合分析的重要性 | 利用数值与理论分析方法,讨论地下水压力对岩体强度与渗透演化的联动机制 | 认为单一考虑水压力不足以解释实际渗流现象,应从渗流-应力耦合视角开展系统研究,以更全面理解地下水活动及其对岩体结构的影响 |
| 左宇军等[ | 研究不同渗透压差与地应力条件下,页岩试样的渗透性演化过程 | 采用应力-应变控制渗透性试验,测定不同压力组合下的渗透系数变化 | 在相同渗透压差条件下,渗透率随地应力增大而降低;在相同地应力下,渗透率随渗透压差增大而升高,说明渗透驱动力和地应力共同调控裂隙渗流行为 |
| 研究学者 | 研究内容 | 实验方法 | 主要结论 |
|---|---|---|---|
| Yi等[ | THMC耦合下裂隙岩石开裂行为 | 设计三轴压缩试验,研究不同THMC场对预制裂纹红砂岩力学行为和破坏模式的影响;采用新提出的THMC断裂准则分析裂纹起裂机制 | 温度升高导致弹性模量下降、起裂应力下降、峰值强度下降;破坏模式由剪切转为拉伸;温度升高削弱断裂韧性,影响裂纹起裂 |
| Li等[ | 基于细观结构DEM建模与机器学习的裂隙岩石THM效应跨尺度分析 | 开发耦合热-水-细观结构的DEM模型T-H-MSBM,模拟不同损伤程度的裂隙花岗岩在THM耦合条件下的压缩行为,结合机器学习建立宏观强度与THM因素的关联数据库 | 温度对力学性质的劣化效应随损伤度增加而放大;低损伤岩石温度依赖性更显著 |
| Wu等[ | 单裂隙岩石THM耦合试验系统的开发与应用 | 研制THM耦合试验系统,包含加载、剪切-渗流箱、高温环境箱和渗流系统,对花岗岩单裂隙进行加热-冷却渗流试验和剪切-渗流耦合试验 | 加热至120 ℃引起热膨胀导致法向位移增加(0.84 mm);CND边界下热应力达初始应力3倍 |
| Liang等[ | 耦合THM环境下盐岩渗透率与孔隙结构演化及其自愈合机制 | 利用自研高地应力高温THM耦合设备处理盐岩,通过显微CT(MCT)和金相显微镜观察孔隙、裂隙演化,对比仅热处理的盐岩特性 | 400~500 ℃:愈合主导导致渗透率下降;500 ℃以上:损伤主导导致渗透率上升;最佳愈合区间:400~500 ℃ |
| Meng等[ | 耦合THM环境下裂隙岩石渗透率演化与非线性渗流特性实验研究(以西山沉积岩为例) | 设计THM耦合三轴试验装置,研究实时超高温(20~650 ℃)和三轴应力(地应力 5~25 MPa)下裂隙岩石的渗透率演化,采用DIC技术和3D激光扫描分析裂隙孔径与粗糙度 | 渗透率拐点:300 ℃/500 ℃;300 ℃以上引起侧向变形导致流量骤升;500 ℃以上导致渗流各向异性降低 |
| Huang等[ | 耦合THM条件下储层岩石裂纹量化与渗透率演化:设备开发与实验研究 | 研制X射线兼容的THM耦合三轴装置,对煤样进行三轴应力循环和渗透率实验,结合CT扫描分析裂纹演化与渗透率的关系 | 裂纹面积分数随应力循环增加导致渗透率上升;高温促进裂纹扩展 |
| Meng等[ | 耦合THM环境处理后盐岩的 II 型断裂特性与粗糙度研究 | 用自研THM耦合三轴仪预处理盐岩,进行三点弯曲(SCB)试验,利用DIC技术、3D激光扫描和电镜分析断裂过程区长度、断裂表面形貌及粗糙度 | 500 ℃以上导致断裂韧性下降;温度升高引起微裂纹增加,裂尖过程区长度增加(1.32~3.59 mm) |
| Zhang等[ | 研究EGS裂隙在热采阶段热应力/热破裂作用下的渗透率演化及损伤机制,分析温度、地应力、注入速度等因素的影响 | 自开发高温渗流实验装置,进行50~200 ℃长期渗透率测试;构建THM-D耦合模型模拟裂隙损伤分布;通过CT扫描观察热破裂后裂隙形态及碎屑分布 | 200 ℃:热破裂导致渗透率先上升后下降(碎屑堵塞);基质热破裂受注入速度和非均质性促进 |
| Meng等[ | 研究大理石在 25~600 ℃高温THM耦合环境(25 MPa 三轴应力、6 MPa 渗流压力)下的渗透率及孔隙结构演化,对比单纯热处理(HTO)的影响 | 高地应力高温THM耦合试验机进行渗透率测试;微CT 扫描和压汞实验分析孔隙参数(孔隙度、孔径分布、分形维数);岩石薄片显微观察热损伤裂隙形态 | THM下渗透率变化:25~400 ℃缓慢上升,400~550 ℃波动,和550 ℃以上快速上升;大理石在THM下经历 “热弹性变形→弹塑性流动→热分解” 三阶段,550 ℃以上石英相变导致渗透率骤升 |
| Wu等[ | 研究超高温(25~650 ℃)EGS 储层在THM耦合环境下的渗透率及孔隙结构演化规律,分析温度阶段对微观参数的影响机制 | 自设计THM耦合测试系统(25 MPa三轴应力和6 MPa 渗流压力);压汞实验、微CT扫描和薄片显微分析孔隙结构;分形维数定量表征孔隙复杂性 | THM下渗透率变化:25~400 ℃缓慢增加,400~550 ℃波动,550~650 ℃骤升;高温(>550 ℃)岩石破坏;573 ℃石英相变导致体积膨胀,触发宏观裂隙,渗透率提升 122% |
表3 温度耦合地下水渗流的实验与数值研究
Table 3 Experimental and numerical study on thermally coupled groundwater seepage
| 研究学者 | 研究内容 | 实验方法 | 主要结论 |
|---|---|---|---|
| Yi等[ | THMC耦合下裂隙岩石开裂行为 | 设计三轴压缩试验,研究不同THMC场对预制裂纹红砂岩力学行为和破坏模式的影响;采用新提出的THMC断裂准则分析裂纹起裂机制 | 温度升高导致弹性模量下降、起裂应力下降、峰值强度下降;破坏模式由剪切转为拉伸;温度升高削弱断裂韧性,影响裂纹起裂 |
| Li等[ | 基于细观结构DEM建模与机器学习的裂隙岩石THM效应跨尺度分析 | 开发耦合热-水-细观结构的DEM模型T-H-MSBM,模拟不同损伤程度的裂隙花岗岩在THM耦合条件下的压缩行为,结合机器学习建立宏观强度与THM因素的关联数据库 | 温度对力学性质的劣化效应随损伤度增加而放大;低损伤岩石温度依赖性更显著 |
| Wu等[ | 单裂隙岩石THM耦合试验系统的开发与应用 | 研制THM耦合试验系统,包含加载、剪切-渗流箱、高温环境箱和渗流系统,对花岗岩单裂隙进行加热-冷却渗流试验和剪切-渗流耦合试验 | 加热至120 ℃引起热膨胀导致法向位移增加(0.84 mm);CND边界下热应力达初始应力3倍 |
| Liang等[ | 耦合THM环境下盐岩渗透率与孔隙结构演化及其自愈合机制 | 利用自研高地应力高温THM耦合设备处理盐岩,通过显微CT(MCT)和金相显微镜观察孔隙、裂隙演化,对比仅热处理的盐岩特性 | 400~500 ℃:愈合主导导致渗透率下降;500 ℃以上:损伤主导导致渗透率上升;最佳愈合区间:400~500 ℃ |
| Meng等[ | 耦合THM环境下裂隙岩石渗透率演化与非线性渗流特性实验研究(以西山沉积岩为例) | 设计THM耦合三轴试验装置,研究实时超高温(20~650 ℃)和三轴应力(地应力 5~25 MPa)下裂隙岩石的渗透率演化,采用DIC技术和3D激光扫描分析裂隙孔径与粗糙度 | 渗透率拐点:300 ℃/500 ℃;300 ℃以上引起侧向变形导致流量骤升;500 ℃以上导致渗流各向异性降低 |
| Huang等[ | 耦合THM条件下储层岩石裂纹量化与渗透率演化:设备开发与实验研究 | 研制X射线兼容的THM耦合三轴装置,对煤样进行三轴应力循环和渗透率实验,结合CT扫描分析裂纹演化与渗透率的关系 | 裂纹面积分数随应力循环增加导致渗透率上升;高温促进裂纹扩展 |
| Meng等[ | 耦合THM环境处理后盐岩的 II 型断裂特性与粗糙度研究 | 用自研THM耦合三轴仪预处理盐岩,进行三点弯曲(SCB)试验,利用DIC技术、3D激光扫描和电镜分析断裂过程区长度、断裂表面形貌及粗糙度 | 500 ℃以上导致断裂韧性下降;温度升高引起微裂纹增加,裂尖过程区长度增加(1.32~3.59 mm) |
| Zhang等[ | 研究EGS裂隙在热采阶段热应力/热破裂作用下的渗透率演化及损伤机制,分析温度、地应力、注入速度等因素的影响 | 自开发高温渗流实验装置,进行50~200 ℃长期渗透率测试;构建THM-D耦合模型模拟裂隙损伤分布;通过CT扫描观察热破裂后裂隙形态及碎屑分布 | 200 ℃:热破裂导致渗透率先上升后下降(碎屑堵塞);基质热破裂受注入速度和非均质性促进 |
| Meng等[ | 研究大理石在 25~600 ℃高温THM耦合环境(25 MPa 三轴应力、6 MPa 渗流压力)下的渗透率及孔隙结构演化,对比单纯热处理(HTO)的影响 | 高地应力高温THM耦合试验机进行渗透率测试;微CT 扫描和压汞实验分析孔隙参数(孔隙度、孔径分布、分形维数);岩石薄片显微观察热损伤裂隙形态 | THM下渗透率变化:25~400 ℃缓慢上升,400~550 ℃波动,和550 ℃以上快速上升;大理石在THM下经历 “热弹性变形→弹塑性流动→热分解” 三阶段,550 ℃以上石英相变导致渗透率骤升 |
| Wu等[ | 研究超高温(25~650 ℃)EGS 储层在THM耦合环境下的渗透率及孔隙结构演化规律,分析温度阶段对微观参数的影响机制 | 自设计THM耦合测试系统(25 MPa三轴应力和6 MPa 渗流压力);压汞实验、微CT扫描和薄片显微分析孔隙结构;分形维数定量表征孔隙复杂性 | THM下渗透率变化:25~400 ℃缓慢增加,400~550 ℃波动,550~650 ℃骤升;高温(>550 ℃)岩石破坏;573 ℃石英相变导致体积膨胀,触发宏观裂隙,渗透率提升 122% |
| 模型类型 | 主要特点 | 优点 | 局限性 | 典型适用工程条件 |
|---|---|---|---|---|
| 解析模型 | 基于理论推导,结构简洁 | 物理意义清晰,计算效率高 | 难以处理复杂几何与非均质性 | 单裂隙或规则裂隙系统 |
| 数值模型 | 可模拟复杂边界和多场耦合 | 精度高,适用性广 | 计算量大,需较多参数输入 | 深部工程渗流、储层预测 |
| 经验模型 | 基于实验/现场回归关系 | 便于快速预测,计算简便 | 缺乏物理机制支撑,外推性有限 | 工程现场快速估算与参数反演 |
| 机器学习 | 数据驱动,自动提取特征 | 可处理高维非线性 问题,预测效率高 | 需大量高质量数据, 物理解释性较弱 | 裂隙网络建模、 大规模数据预测 |
表4 不同模型的适用条件与应用场景总结
Table 4 Summary of applicable conditions and application scenarios of different models
| 模型类型 | 主要特点 | 优点 | 局限性 | 典型适用工程条件 |
|---|---|---|---|---|
| 解析模型 | 基于理论推导,结构简洁 | 物理意义清晰,计算效率高 | 难以处理复杂几何与非均质性 | 单裂隙或规则裂隙系统 |
| 数值模型 | 可模拟复杂边界和多场耦合 | 精度高,适用性广 | 计算量大,需较多参数输入 | 深部工程渗流、储层预测 |
| 经验模型 | 基于实验/现场回归关系 | 便于快速预测,计算简便 | 缺乏物理机制支撑,外推性有限 | 工程现场快速估算与参数反演 |
| 机器学习 | 数据驱动,自动提取特征 | 可处理高维非线性 问题,预测效率高 | 需大量高质量数据, 物理解释性较弱 | 裂隙网络建模、 大规模数据预测 |
| [1] |
陈喜, 董建志, 王礼春, 等. 全球变化下生态水文学发展与展望[J]. 地学前缘, 2025, 32(3): 52-61.
DOI |
| [2] | 钱家忠, 吴剑锋, 朱学愚, 等. 地下水资源评价与管理数学模型的研究进展[J]. 科学通报, 2001, 46(2): 99-104. |
| [3] | 王京平. 围压耦合渗流机理特性的实验与理论研究[D]. 合肥: 合肥工业大学, 2022. |
| [4] | 张庆. 高水压和围压温度耦合作用下压裂裂隙渗流特性研究[D]. 焦作: 河南理工大学, 2021. |
| [5] |
黄永辉, 庞忠和, 程远志, 等. 深层含水层地下储热技术的发展现状与展望[J]. 地学前缘, 2020, 27(1): 17-24.
DOI |
| [6] |
SHU B, ZHU R, ELSWORTH D, et al. Effect of temperature and confining pressure on the evolution of hydraulic and heat transfer properties of geothermal fracture in granite[J]. Applied Energy, 2020, 272: 115290.
DOI URL |
| [7] |
GHABEZLOO S, SULEM J. Stress dependent thermal pressurization of a fluid-saturated rock[J]. Rock Mechanics and Rock Engineering, 2009, 42: 1-24.
DOI URL |
| [8] |
ZOU L, CVETKOVIC V. Disposal of high-level radioactive waste in crystalline rock: on coupled processes and site development[J]. Rock Mechanics Bulletin, 2023, 2(3): 100061.
DOI URL |
| [9] | 李露露, 张秋兰, 李星宇, 等. 高放废物深地质处置地下水数值模拟应用综述[J]. 水文地质工程地质, 2022, 49(2): 43-53. |
| [10] | 罗晓容, 张立宽, 付晓飞, 等. 深层油气成藏动力学研究进展[J]. 矿物岩石地球化学通报, 2016, 35(5): 876-889, 806. |
| [11] | 李忠, 李佳蔚, 张平童, 等. 深层碳酸盐岩关键构造-流体演变与成岩-成储: 以塔中奥陶系鹰山组为例[J]. 矿物岩石地球化学通报, 2016, 35(5): 827-838. |
| [12] | SNOW D T. A parallel plate model of fractured permeable media[D]. Berkeley: University of California, 1965. |
| [13] | ZHANG S, LIU X, WANG E, et al. A novel model of hydraulic aperture for rough single fracture: insights from fluid inertial and fracture geometry effects[J]. Journal of Geophysical Research: Solid Earth, 2024, 129(7): e2024JB029018. |
| [14] |
HE X, SINAN M, KWAK H, et al. A corrected cubic law for single-phase laminar flow through rough-walled fractures[J]. Advances in Water Resources, 2021, 154: 103984.
DOI URL |
| [15] | MURATA S, SAITO T. Estimation of tortuosity of fluid flow through a single fracture[J]. Journal of Canadian Petroleum Technology, 2003, 42(12): 39-45. |
| [16] | WANG L, CARDENAS M B, ZHOU J Q, et al. The complexity of nonlinear flow and non-Fickian transport in fractures driven by three-dimensional recirculation zones[J]. Journal of Geophysical Research: Solid Earth, 2020, 125(9): e2020JB020028. |
| [17] |
ZHANG Z, NEMCIK J, QIAO Q, et al. A model for water flow through rock fractures based on friction factor[J]. Rock Mechanics and Rock Engineering, 2015, 48: 559-571.
DOI URL |
| [18] |
BARTON N, WANG C, YONG R. Advances in joint roughness coefficient (JRC) and its engineering applications[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2023, 15(12): 3352-3379.
DOI URL |
| [19] |
WANG J, MA H, QIAN J, et al. Experimental and theoretical study on the seepage mechanism characteristics coupling with confining pressure[J]. Engineering Geology, 2021, 291: 106224.
DOI URL |
| [20] |
FENG P, MA H, QIAN J, et al. Mesoscopic study of seepage characteristics with shear displacement in a single fracture[J]. Acta Geophysica, 2024, 72(4): 2619-2632.
DOI |
| [21] | MA H, WEI X, HU G, et al. Seepage disturbance mechanism and interface force of cylindrical barrier in fracture[J]. Physics of Fluids, 2024, 36(3): 035604. |
| [22] |
LI J, CHEN S, WU R, et al. A novel semi-theoretical model for hydraulic conductivity prediction considering temperature effect[J]. Case Studies in Thermal Engineering, 2025, 71: 106188.
DOI URL |
| [23] |
LAVROV A. Flow of non-Newtonian fluids in single fractures and fracture networks: current status, challenges, and knowledge gaps[J]. Engineering Geology, 2023, 321: 107166.
DOI URL |
| [24] |
HOUBEN G, WEITKAMP A, KAUFHOLD S. The roughness of fracture surfaces and its scale dependence-a methodological study based on natural fractures in sandstones from Southern Germany[J]. Environmental Earth Sciences, 2024, 83(13): 388.
DOI |
| [25] |
WEN Z, LIU K, CHEN X. Approximate analytical solution for non-Darcian flow toward a partially penetrating well in a confined aquifer[J]. Journal of Hydrology, 2013, 498: 124-131.
DOI URL |
| [26] |
ZHU Q, WEN Z, JAKADA H. A new solution to transient single-well push-pull test with low-permeability non-Darcian leakage effects[J]. Journal of Contaminant Hydrology, 2020, 234: 103689.
DOI URL |
| [27] | XING K, QIAN J, MA H, et al. Characterizing the relationship between non-Darcy effect and hydraulic aperture in rough single fractures[J]. Water Resources Research, 2021, 57(9): e2021WR030451. |
| [28] |
PYRAK-NOLTE L J, NOLTE D D. Approaching a universal scaling relationship between fracture stiffness and fluid flow[J]. Nature Communications, 2016, 7(1): 10663.
DOI |
| [29] |
WANG J, MA H, FENG P, et al. An experimental study on seepage within shale fractures due to confining pressure and temperature[J]. KSCE Journal of Civil Engineering, 2021, 25(9): 3596-3604.
DOI URL |
| [30] |
MA H, WANG J, QIAN J, et al. Effects of confining pressure on permeability in a single fracture based on the deformation of hydraulic aperture at low fluid velocities[J]. Lithosphere, 2022, 2022(1): 4655543.
DOI URL |
| [31] |
MA H, WANG J, FENG P, et al. Effect of high confining pressure on flow behavior and hydraulic aperture considering fractured rock deformation[J]. Geomechanics and Geophysics for Geo-Energy and Geo-Resources, 2022, 8(5): 155.
DOI |
| [32] |
MA H, WANG J, QIAN J, et al. Mesoscopic deformation of a hydraulic and mechanical aperture of a single fracture under normal stress[J]. Lithosphere, 2023, 2023(1): 1118957.
DOI URL |
| [33] |
蔡振忠, 赵海涛, 王彭, 等. 考虑流固耦合作用的超深缝洞型碳酸盐岩储层连通性表征: 以塔里木盆地富满油田满深区块为例[J]. 地学前缘, 2024, 31(5): 301-312.
DOI |
| [34] | FORCHHEIMER P H. Wasserbewegung durch boden[J]. Zeitschrift des Vereines Deutscher Ingenieure, 1901, 45(50): 1781-1788. |
| [35] | ROSE H E. Fluid flow through beds of granular material[C]// Some aspects of fluid flow: papers presented at a conference of the institute of physics. London: Edward Arnold & Co., 1951: 136-163. |
| [36] | POLUBARINOVA-KOCHINA P Y. Theory of ground water movement[M]. Princeton: Princeton University Press, 2015. |
| [37] | MUSKAT M. The flow of homogeneous fluids through porous media[J]. Soil Science, 1938, 46(2): 169. |
| [38] | HARR M E. Groundwater and seepage[M]. North Chelmsford: Courier Corporation, 1991. |
| [39] | IZBASH S V. O filtracii v kropnozernstom materiale[R]. USSR (in Russian): Leningrad, 1931. |
| [40] | ESCANDE L. Experiments concerning the infiltration of water through a rock mass[C]// Proceedings of Minnesota International Hydraulic Convention. Reston: ASCE, 1953: 547-553. |
| [41] | WILKINS J K. Flow of water through rock fill and its application to the design of dams[J]. New Zealand Engineering, 1955, 10(11): 382-387. |
| [42] | SLEPICKA F. Hydraulic function of cylindrical well in an artesian aquifer with regard to new research on flow through porous media[C]// Proceedings of the 9th World Congress of the International Association of Hydraulic Research. held at Dubrovnik, Czechoslovakia, 1961: 1. |
| [43] | STEPHENSON D J. Rockfill in hydraulic engineering[M]. Netherlands: Elsevier, 1979. |
| [44] |
LASSEUX D, ABBASIAN ARANI A A, AHMADI A. On the stationary macroscopic inertial effects for one phase flow in ordered and disordered porous media[J]. Physics of Fluids, 2011, 23(7): 073103.
DOI URL |
| [45] |
AGNAOU M, LASSEUX D, AHMADI A. Origin of the inertial deviation from Darcy’s law: an investigation from a microscopic flow analysis on two-dimensional model structures[J]. Physical Review E, 2017, 96(4): 043105.
DOI URL |
| [46] |
BORDIER C, ZIMMER D. Drainage equations and non-Darcian modelling in coarse porous media or geosynthetic materials[J]. Journal of Hydrology, 2000, 228(3/4): 174-187.
DOI URL |
| [47] |
WEN Z, HUANG G, ZHAN H. Non-Darcian flow in a single confined vertical fracture toward a well[J]. Journal of Hydrology, 2006, 330(3/4): 698-708.
DOI URL |
| [48] |
QUINN P M, CHERRY J A, PARKER B L. Relationship between the critical Reynolds number and aperture for flow through single fractures: evidence from published laboratory studies[J]. Journal of Hydrology, 2020, 581: 124384.
DOI URL |
| [49] | ZIMMERMAN R W, BODVARSSON G S. Hydraulic conductivity of rock fractures[J]. Transport in Porous Media, 1996, 23: 1-30. |
| [50] | BRUSH D J, THOMSON N R. Fluid flow in synthetic rough-walled fractures: navier-stokes, stokes, and local cubic law simulations[J]. Water Resources Research, 2003, 39(4): 1085. |
| [51] |
YU X, ZHANG T, YANG K, et al. Quantitative characterization of seepage behavior in rough fracture considering hydromechanical coupling effect: an experimental study[J]. Acta Geophysica, 2023, 71(5): 2245-2264.
DOI |
| [52] |
JAVADI M, SHARIFZADEH M, SHAHRIAR K, et al. Critical Reynolds number for nonlinear flow through rough-walled fractures: the role of shear processes[J]. Water Resources Research, 2014, 50(2): 1789-1804.
DOI URL |
| [53] |
QIAN J, ZHAN H, ZHAO W, et al. Experimental study of turbulent unconfined groundwater flow in a single fracture[J]. Journal of Hydrology, 2005, 311(1/2/3/4): 134-142.
DOI URL |
| [54] |
YAO Y, LI G, QIN P. Seepage features of high-velocity non-Darcy flow in highly productive reservoirs[J]. Journal of Natural Gas Science and Engineering, 2015, 27: 1732-1738.
DOI URL |
| [55] | KONZUK J S, KUEPER B H. Evaluation of cubic law based models describing single-phase flow through a rough-walled fracture[J]. Water Resources Research, 2004, 40(2): W02402. |
| [56] |
MONTROLL E W, WEISS G H. Random walks on lattices. II[J]. Journal of Mathematical Physics, 1965, 6(2): 167-181.
DOI URL |
| [57] | BERKOWITZ B, CORTIS A, DENTZ M, et al. Modeling non-Fickian transport in geological formations as a continuous time random walk[J]. Reviews of Geophysics, 2006, 44(2): RG2003. |
| [58] | MILLER K S, ROSS B. An introduction to the fractional calculus and fractional differential equations[M]. Hoboken: John Wiley, 1993. |
| [59] | SAMORADNITSKY G. Stable non-Gaussian random processes: stochastic models with infinite variance[M]. Oxford: Routledge, 2017. |
| [60] | PACHEPSKY Y, TIMLIN D, BENSON D A. Transport of water and solutes in soils as in fractal porous media[J]. Physical and Chemical Processes of Water and Solute Transport/Retention in Soils, 2001, 56: 51-75. |
| [61] |
VOLLER V R. On a fractional derivative form of the Green-Ampt infiltration model[J]. Advances in Water Resources, 2011, 34(2): 257-262.
DOI URL |
| [62] |
MA H, CAO Y, QIAN J, et al. Theoretical study of the mesoscopic mechanism of rock fractures during normal deformation[J]. Rock Mechanics and Rock Engineering, 2023, 56(8): 5719-5733.
DOI |
| [63] | MA H, CAO Y, QIAN J, et al. Study on mechanism of rock joint normal deformation based on mesoscopic modified hertzian contact model[J]. Rock Mechanics and Rock Engineering, 2024, 57: 1-19. |
| [64] |
ZHANG A, YANG J, CHENG L, et al. A simulation study on stress-seepage characteristics of 3D rough single fracture based on fluid-structure interaction[J]. Journal of Petroleum Science and Engineering, 2022, 211: 110215.
DOI URL |
| [65] | LIU X, ZHANG J, ZHOU X, et al. Damage-seepage evolution mechanism of fractured rock masses considering the influence of lateral stress on fracture deformation under loading and unloading process[J]. Rock Mechanics and Rock Engineering, 2024, 57: 1-27. |
| [66] |
FIDELIBUS C. The 2D hydro-mechanically coupled response of a rock mass with fractures via a mixed BEM-FEM technique[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2007, 31(11): 1329-1348.
DOI URL |
| [67] | ZHANG Y, WU X, WU Q, et al. Investigation of permeability characteristics of rock under confining pressure-fracture coupling conditions[J]. Rock Mechanics and Rock Engineering, 2025 (58): 1-17. |
| [68] |
FENG Z, ZHAO Y, LIU D. Permeability evolution of thermally cracked granite with different grain sizes[J]. Rock Mechanics and Rock Engineering, 2021, 54: 1953-1967.
DOI |
| [69] | SUMMERS R, WINKLER K, BYERLEE J. Permeability changes during the flow of water through Westerly Granite at temperatures of 100-400 ℃[J]. Journal of Geophysical Research: Solid Earth, 1978, 83(B1): 339-344. |
| [70] |
KUMARI W G P, RANJITH P G. Experimental and numerical investigation of the flow behaviour of fractured granite under extreme temperature and pressure conditions[J]. Sustainability, 2022, 14(14): 8587.
DOI URL |
| [71] |
FENG R, CHEN S, BRYANT S, et al. Stress-dependent permeability measurement techniques for unconventional gas reservoirs: review, evaluation, and application[J]. Fuel, 2019, 256: 115987.
DOI URL |
| [72] | 王恩志, 张文韶, 韩小妹, 等. 低渗透岩石在围压作用下的耦合渗流实验[J]. 清华大学学报: 自然科学版, 2005, 45(6): 764-767. |
| [73] | 徐德敏, 黄润秋, 张强, 等. 高围压条件下孔隙介质渗透特性试验研究[J]. 工程地质学报, 2007, 15(6): 752-756. |
| [74] | 蒋宇静, 李博, 王刚, 等. 岩石裂隙渗流特性试验研究的新进展[J]. 岩石力学与工程学报, 2008, 27(12): 2377-2386. |
| [75] | 王俊光, 梁冰. 渗透动水压力作用下裂隙岩体渗流与应力耦合分析[J]. 辽宁工程技术大学学报 (自然科学版), 2009, 28(增刊1): 178-180. |
| [76] | 刘杰, 李建林, 王瑞红, 等. 含密实原岩充填物的宜昌砂岩裂隙渗流试验研究[J]. 岩石力学与工程学报, 2010(2): 366-374. |
| [77] | 刘欣宇. 含充填裂隙类岩石高围压条件下水渗流试验研究[D]. 长沙: 中南大学, 2012. |
| [78] | 左宇军, 孙文, 吉斌, 等. 渗透压-应力耦合作用下页岩渗透性试验[J]. 岩土力学, 2018, 39(9): 3253-3260. |
| [79] |
PAN P Z, RUTQVIST J, FENG X T, et al. An approach for modeling rock discontinuous mechanical behavior under multiphase fluid flow conditions[J]. Rock Mechanics and Rock Engineering, 2014, 47: 589-603.
DOI URL |
| [80] | LI L C, TANG C A, LI G, et al. Numerical simulation of 3D hydraulic fracturing based on an improved flow-stress-damage model and a parallel FEM technique[J]. Rock Mechanics and rock engineering, 2012, 45: 801-818. |
| [81] | FANG Z, HARRISON J P. Development of a local degradation approach to the modelling of brittle fracture in heterogeneous rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(4): 443-457. |
| [82] | MA G W, WANG X J, REN F. Numerical simulation of compressive failure of heterogeneous rock-like materials using SPH method[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(3): 353-363. |
| [83] | YI W, HUANG S, RAO Q, et al. Cracking behaviors and mechanism of pre-cracked rock specimens under coupled THM fields with chemical processes[J]. Case Studies in Construction Materials, 2024, 20: e02758. |
| [84] |
LI M, WU Z, WENG L, et al. Cross-scale analysis for the thermo-hydro-mechanical (THM) effects on the mechanical behaviors of fractured rock: integrating mesostructure-based DEM modeling and machine learning[J]. Engineering Fracture Mechanics, 2024, 306: 110204.
DOI URL |
| [85] |
WU R, CHEN S, WANG G, et al. Development and application of a thermo-hydro-mechanical coupling test system for a single rock fracture[J]. Measurement, 2025, 242: 116197.
DOI URL |
| [86] |
LIANG X, MENG T, FENG G, et al. Evolution of permeability and pore structure of salt rock and its self-healing mechanism under coupled thermo-hydro-mechanical environment[J]. Journal of Energy Storage, 2023, 66: 107476.
DOI URL |
| [87] |
MENG T, LIFENG M, FENGBIAO W, et al. Experimental study on permeability evolution and nonlinear seepage characteristics of fractured rock in coupled thermo-hydraulic-mechanical environment: a case study of the sedimentary rock in Xishan area[J]. Engineering Geology, 2021, 294: 106339.
DOI URL |
| [88] |
HUANG J, SONG Z, LIAO Z, et al. Quantification of cracks and the evolution of permeability for reservoir rock under coupled THM: equipment development and experimental research[J]. Geomechanics and Geophysics for Geo-Energy and Geo-Resources, 2020, 6: 1-13.
DOI |
| [89] |
MENG T, WANG T, GUO K, et al. Study of mode II fracture characteristics and roughness in salt rock after treatment coupled thermo-hydro-mechanical environment[J]. Engineering Fracture Mechanics, 2023, 291: 109572.
DOI URL |
| [90] |
ZHANG W, WANG D, WANG Z, et al. Study on permeability evolution and damage mechanism along the EGS fracture in heat mining stage under thermal stress/cracking[J]. Geothermal Energy, 2023, 11(1): 31.
DOI |
| [91] |
MENG T, ZHANG Z, TAHERDANGKOO R, et al. Temperature-dependent evolution of permeability and pore structure of marble under a high-temperature thermo-hydro-mechanical coupling environment[J]. Acta Geotechnica, 2024, 19(9): 5967-5988.
DOI |
| [92] |
WU F, ZHANG D, MA L, et al. Thermo-hydro-mechanical (THM) evolution law and development of permeability and pore structure of enhanced geothermal systems at ultra-high temperatures[J]. Geothermics, 2021, 97: 102253.
DOI URL |
| [1] | 文章, 李一鸣, 郭绪磊, 万坦, 罗清树, 周宏. 葛洲坝库区裂隙河岸地表水-地下水交互特征[J]. 地学前缘, 2026, 33(1): 1-13. |
| [2] | 曲辞晓, 王明玉. 裂隙介质VOCs传输扩散通量高效预测建模框架及突破点探析[J]. 地学前缘, 2026, 33(1): 207-221. |
| [3] | 董艳辉, 王礼恒, 张倩, 周志超, 文冬光, 李守定, 万力. 深部水文地质学裂隙渗流研究挑战与进展[J]. 地学前缘, 2026, 33(1): 296-312. |
| [4] | 周斐然, 尹子悦, 孙晓敏, 宋健, 杨蕴, 吴剑锋. 融合数值模拟和机器学习的民勤盆地地下水潜力评价与主控因素识别[J]. 地学前缘, 2026, 33(1): 511-522. |
| [5] | 何晓, 牛花朋, 赵贤, 周浩彦, 林伟峻, 张关龙, 孟涛, 穆星. 基于数值模拟表征岩石组构对裂缝性储层发育影响程度的机理研究:以济阳坳陷花岗质岩石为例[J]. 地学前缘, 2025, 32(5): 361-376. |
| [6] | 胡景宏, 廖松泽, 蔡益栋, 芦俊. 深部页岩储层压裂裂缝扩展均匀性研究[J]. 地学前缘, 2025, 32(4): 471-482. |
| [7] | 肖昀廷, 蔡晨康, 黄亦心, 朱佳雷. 海表温度日变化特征对海陆风模拟的影响研究[J]. 地学前缘, 2025, 32(3): 218-230. |
| [8] | 余路, 李贤, 崔国栋, 邢东辉, 陆红锋, 王烨嘉. 启动压力对南海北部水合物藏开发动态的影响[J]. 地学前缘, 2025, 32(2): 178-194. |
| [9] | 杨冰, 孟童, 郭华明, 连国玺, 陈帅瑶, 杨曦. 基于Kd的某酸法地浸铀矿山地下水铀运移模拟[J]. 地学前缘, 2024, 31(3): 381-391. |
| [10] | 侯玉松, 胡晓农, 吴吉春. 不同胶结度的多孔介质中溶质横向弥散的孔隙尺度模拟研究[J]. 地学前缘, 2024, 31(3): 59-67. |
| [11] | 李玉丹, 游瑜春, 曾大乾, 石志良, 顾少华, 张睿. 底水气藏水侵规律数值模拟研究:以元坝长兴组气藏为例[J]. 地学前缘, 2023, 30(6): 341-350. |
| [12] | 张允, 康志江, 马郡伟, 郑欢, 吴大卫. 深层离散裂缝油藏多尺度流固耦合数值模拟方法[J]. 地学前缘, 2023, 30(6): 365-370. |
| [13] | 孙哲, 张彬, 陈大伟, 李玉涛, 王汉勋. 花岗岩裂隙岩体油水两相渗流可视化试验及数值模拟研究[J]. 地学前缘, 2023, 30(3): 465-475. |
| [14] | 孙辉, 刘晓东. 青藏高原隆升气候效应的数值模拟研究进展概述[J]. 地学前缘, 2022, 29(5): 300-309. |
| [15] | 沈晓芳, 万玉玉, 王利刚, 苏小四, 董维红. 基于多相流数值模拟的某石油污染场地地下水中VOCs自然衰减过程识别及能力评估[J]. 地学前缘, 2021, 28(5): 90-103. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||