基于集成学习模型与贝叶斯优化算法的成矿预测

doi:10.13745/j.esf.sf.2025.4.66

地学前缘 ›› 2025, Vol. 32 ›› Issue (4): 122-139.DOI: 10.13745/j.esf.sf.2025.4.66

基于集成学习模型与贝叶斯优化算法的成矿预测

孔春芳¹^,²^,³^,⁴(), 田倩¹, 刘健⁵, 蔡国荣¹^,⁵, 赵杰¹, 徐凯¹^,²^,³^,⁴^,^*()

1.中国地质大学(武汉) 计算机学院, 湖北武汉 430074
2.自然资源部基岩区矿产资源勘查工程技术创新中心, 贵州贵阳 550081
3.贵州省战略矿产智慧勘查全省重点实验室, 贵州贵阳 550081
4.智能地学信息处理湖北省重点实验室, 湖北武汉 430074
5.贵州省地质矿产勘查开发局一○三地质大队, 贵州铜仁 554300

收稿日期:2025-05-12 修回日期:2025-05-20 出版日期:2025-07-25 发布日期:2025-08-04
通信作者: *徐凯(1972—),男,博士,副教授,主要从事数据挖掘与知识发现、基于大数据的智能找矿、定量遥感与地学信息工程等方面的教学与研究工作。E-mail: xukai@cug.edu.cn
作者简介:孔春芳(1973—),女,博士,副教授,主要从事遥感与地理信息系统应用方面的教学与科研工作。E-mail: kongcf@cug.edu.cn
基金资助:
贵州省找矿突破战略行动重大协同创新项目(黔科合战略找矿[2022]ZD004);湖北省自然科学基金项目(2021CFB506);智能地学信息处理湖北省重点实验室开放基金项目(KLIGIP-2023-B08);贵州省基础研究计划(自然科学)(QKHJC-ZK[2023]G 194);贵州省重大科技成果转化项目(黔科合[2022]重点003);贵州省地质矿产勘查开发局项目(黔地矿科合[2021]3);贵州省地质矿产勘查开发局项目(黔地矿科合[2023]1);铜仁市科技局科研项目(铜市科研[2024]97号)

Metallogenic prediction based on ensemble learning models and Bayesian Optimization Algorithm

KONG Chunfang¹^,²^,³^,⁴(), TIAN Qian¹, LIU Jian⁵, CAI Guorong¹^,⁵, ZHAO Jie¹, XU Kai¹^,²^,³^,⁴^,^*()

1. School of Computer, China University of Geosciences (Wuhan), Wuhan 430074, China
2. Engineering Technology Innovation Center of Mineral Resource Explorations in Bedrock Zones, Ministry of Natural Resources, Guiyang 550081, China
3. Guizhou Key Laboratory for Strategic Mineral Intelligent Exploration, Guiyang 550081, China
4. Hubei Key Laboratory of Intelligent Geo-Information Processing, Wuhan 430074, China
5. Geology Team 103, Bureau of Geology and Mineral Exploration and Development, Tongren 554300, China

Received:2025-05-12 Revised:2025-05-20 Online:2025-07-25 Published:2025-08-04

摘要/Abstract

摘要：

全球进入隐伏矿体勘查时代,急需新的找矿预测方法。利用集成学习进行的数据驱动的成矿预测模型正在成为深部隐伏矿产勘探的有力工具。然而,基于集成学习的成矿预测模型面临着一些普遍的问题,特别是模型的参数调优。模型的参数调优是一个非常耗时的过程,需要繁琐的计算和足够的专家经验。本文提出了一种基于多源地学知识与贝叶斯优化算法的集成学习模型来解决上述问题。具体来说,首先,基于多源地学知识,构建锰矿成矿预测数据库;其次,基于自适应提升模型(Adaptive Boosting,AdaBoost)和随机森林(Random Forest,RF)模型,建立黔东北锰矿成矿预测模型;然后,采用贝叶斯优化算法(Bayesian Optimization,BO),通过5倍交叉验证的辅助,寻找BO-AdaBoost和BO-RF模型最合适的超参数组合;最后,利用精度、准确率、召回率、F₁分数、kappa系数、AUC值等参数及已有成果检测模型的性能。实验结果发现,BO-AdaBoost和BO-RF模型的AUC值都得到了显著的提高,表明BO是一个强大的优化工具,优化结果为集成学习模型的超参数设置提供了参考。同时,实验结果也表明:BO-AdaBoost模型(92.8%)比BO-RF模型(89.9%)具有更高的预测精度和地质泛化能力,在成矿预测方面具有巨大潜力。基于BO-AdaBoost模型的预测图为黔东北隐伏锰矿矿床的勘探提供了重要线索,并可以指导未来的矿产勘探与开发。

关键词: 集成学习, 自适应提升模型, 随机森林, 贝叶斯优化算法, 隐伏锰矿, 成矿预测

Abstract:

Exploration for hidden ore bodies is increasingly important and demands innovative prospecting methods. Data-driven metallogenic prediction models using ensemble learning are becoming powerful tools for deep mineral exploration. However, such models face challenges, particularly in time-consuming hyperparameter tuning requiring extensive computation and expertise. To address this, we propose a framework integrating multi-source geological knowledge with Bayesian Optimization (BO) for ensemble learning. Specifically, a manganese (Mn) metallogenic prediction database integrating multi-source geological knowledge is first constructed. Metallogenic prediction models for Mn ore in northeastern Guizhou are then established using Adaptive Boosting (AdaBoost) and Random Forest (RF). The hyperparameters of these base models are optimized using Bayesian Optimization (BO) via 5-fold cross-validation, resulting in the optimized BO-AdaBoost and BO-RF models. Model performance is evaluated using metrics including accuracy, precision, recall, F₁-score, kappa, and AUC values. Results show significant improvements in AUC for both BO-optimized models compared to their non-optimized counterparts, demonstrating BO’s effectiveness for ensemble learning hyperparameter tuning. Furthermore, the BO-AdaBoost model achieves higher prediction accuracy (92.8%) and generalization performance than the BO-RF model (89.9%), highlighting its strong potential for metallogenic prediction. The prospectivity map generated by the BO-AdaBoost model provides critical guidance for exploring deep-hidden Mn deposits in northeastern Guizhou and can direct future mineral exploration and development.

Key words: ensemble learning, Adaptive Boosting (AdaBoost), Random Forest (RF), Bayesian Optimization (BO), hidden manganese ore, metallogenic prediction

中图分类号:

孔春芳, 田倩, 刘健, 蔡国荣, 赵杰, 徐凯. 基于集成学习模型与贝叶斯优化算法的成矿预测[J]. 地学前缘, 2025, 32(4): 122-139.

KONG Chunfang, TIAN Qian, LIU Jian, CAI Guorong, ZHAO Jie, XU Kai. Metallogenic prediction based on ensemble learning models and Bayesian Optimization Algorithm[J]. Earth Science Frontiers, 2025, 32(4): 122-139.

图/表 19

图1 基于多源地学知识和贝叶斯优化集成学习方法的锰矿成矿预测流程

Fig.1 Flowchart of the Mn ore metallogenic prediction based on multi-source geological knowledge and Bayesian optimization ensemble learning method

图2 AdaBoost算法流程图

Fig.2 Flowchart of the AdaBoost algorithm

表1 AdaBoost算法步骤

Table 1 The steps of AdaBoost algorithm

步骤	步骤描述
1	标准化、归一化数据集,并按照7∶2∶1的比例分配训练集、测试集和验证集
2	为每一个样本赋予同样的权重,训练出第一个决策树DT₁,让DT₁对样本x_i进行分类得到预测值G₁(x_i),并依据公式 $∑ i = 1 m w k i I (G k (x i) ≠ y i)$ 计算误差率e₁
3	利用误差率e₁进行轮次迭代,依据公式α_k= $1 2 l g (1 - e k) e k$ 来更新分类器本轮次的自身权重α₁,随后结合e₁、α₁以及G₁(x_i),并根据公式(1)和(2)计算出下一轮次每个样本的权重w₂_i。接着依据样本集和样本权重,训练出第二个分类器DT₂,并以此类推
4	不断重复步骤3,共构造15个弱分类器和15个分类器权重α_k。然后使用累加投票法(公式(3))组合成强分类器

表1 AdaBoost算法步骤

Table 1 The steps of AdaBoost algorithm

步骤	步骤描述
1	标准化、归一化数据集,并按照7∶2∶1的比例分配训练集、测试集和验证集
2	为每一个样本赋予同样的权重,训练出第一个决策树DT₁,让DT₁对样本x_i进行分类得到预测值G₁(x_i),并依据公式 $∑ i = 1 m w k i I (G k (x i) ≠ y i)$ 计算误差率e₁
3	利用误差率e₁进行轮次迭代,依据公式α_k= $1 2 l g (1 - e k) e k$ 来更新分类器本轮次的自身权重α₁,随后结合e₁、α₁以及G₁(x_i),并根据公式(1)和(2)计算出下一轮次每个样本的权重w₂_i。接着依据样本集和样本权重,训练出第二个分类器DT₂,并以此类推
4	不断重复步骤3,共构造15个弱分类器和15个分类器权重α_k。然后使用累加投票法(公式(3))组合成强分类器

图3 研究区域地理位置图(a)与构造纲要略图(b)

Fig.3 Geographical location map (a) and structural outline (b) of the study area

图4 武陵次级裂谷构造格架及大塘坡锰矿的空间分析(据文献[1,38]修改) 1—实测与推测断层;2—同生断层;3—锰矿床分布范围;4—超大型锰矿;5—地堑;6—地垒;7—铜仁古裂谷。

Fig.4 Spatial distribution of Datangpo type Mn ore deposits and tectonic framework of Wuling secondary rift. Modified after [1,38].

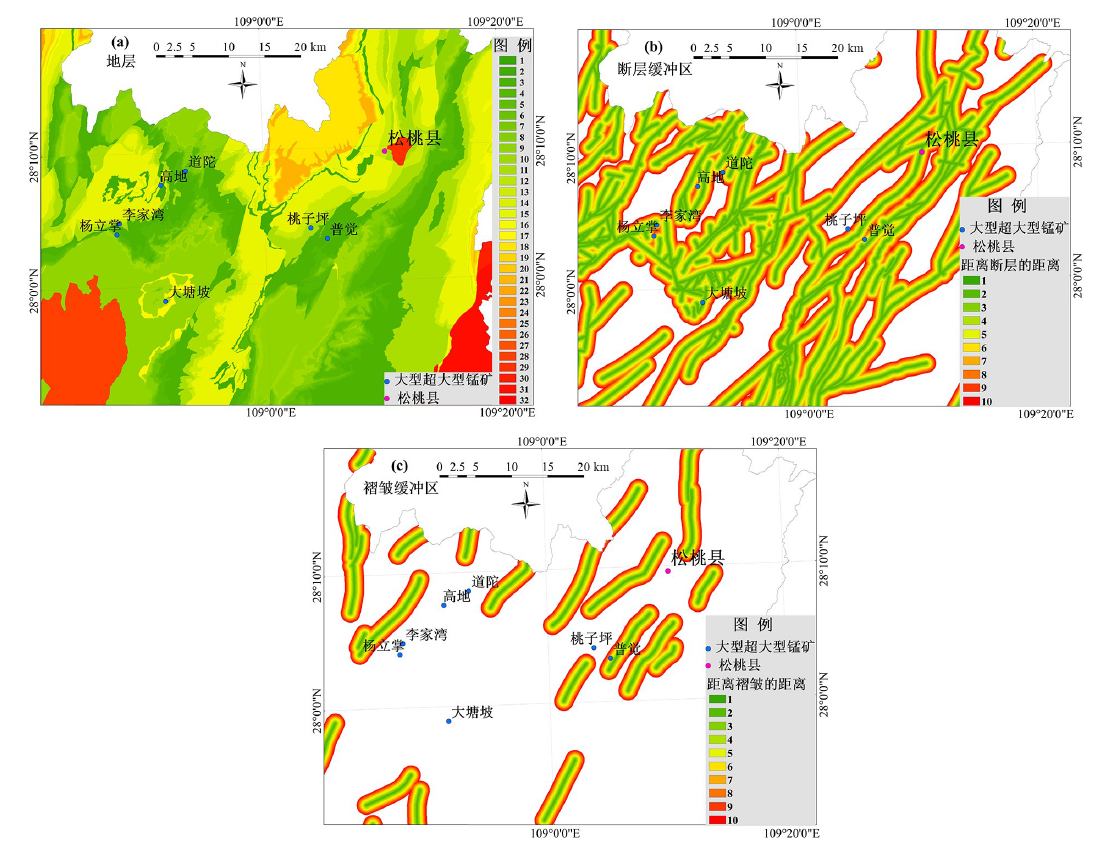
图5 地质变量预测证据层包括地层(a)、断层缓冲区(b)和褶皱缓冲区(c)

Fig.5 The prediction evidence layer for geological variables includes stratum (a), fault buffer zone (b) and (c) fold buffer zone

图6 通过小波分析提取的向下延拓2 km(a)、6 km(b)、10 km(c)和20 km(d)的多尺度地球物理信息

Fig.6 Multiscale geophysical information of 2 km (a), 6 km (b), 10 km (c) and 20 km (d) down-extension extracted by wavelet analysis

图7 通过小波分析提取多尺度航磁ΔT的等值线(a)和ΔT化极等值线(b)

Fig.7 Multi-scale aeromagnetic ΔT contour (a) and polar (b) contour extracted by wavelet analysis

图8 黔东北地区Mn(a)、Cu-As-Co-Cr-Ni(b)、Pb-Zn-Fe-Si(c)和所有元素(d)的地球化学异常图

Fig.8 The geochemical anomaly of Mn (a) Cu-As-Co-Cr-Ni (b) Pb-Zn-Fe-Si (c) and all elements (d) in northeastern Guizhou

图9 基于遥感影像的锰矿化伴生矿物提取结果及异常区分布图(据文献[42]修改)

Fig.9 Extraction results and abnormal area distribution of Mn mineralization associated minerals based on remote sensing

图10 为训练机器学习模型而准备的手动标记的矿点与非矿点的空间分布

Fig.10 Spatial distribution of manually labeled mineral and non-mineral spots for training machine learning model

表2 贝叶斯优化随机森林模型的超参数的过程及结果

Table 2 Hyperparameters optimization process and result of BO-RF model

序号	精度	max_depth	max_features	min_samples_split	n_estimators
1	0.882	9	0.754	8	137
2	0.893	17	0.890	19	174
3	0.899	12	0.920	10	120
4	0.893	16	0.254	16	109
5	0.892	16	0.493	15	182
6	0.898	15	0.944	5	162
7	0.894	13	0.797	18	123
8	0.889	11	0.927	17	72
9	0.885	19	0.729	9	82
10	0.755	1	0.835	7	20
11	0.896	20	0.100	20	10
12	0.895	7	0.120	10	149
13	0.895	14	0.100	20	10
14	0.897	9	0.100	2	119
15	0.894	8	0.990	20	49
16	0.894	20	0.100	2	200
Best	0.899	12	0.920	10	120

表3 Geo-AdaBoost模型的贝叶斯超参数优化过程及结果

Table 3 Hyperparameters optimization process and result of BO-AdaBoost model

序号	精度	max_depth	learning_rate	min_samples_split	min_samples_leaf	n_estimators
1	0.911	5	0.322	19	15	137
2	0.903	9	0.951	7	18	174
3	0.908	5	0.87	4	18	146
4	0.911	8	0.804	13	4	109
5	0.914	8	0.718	11	9	182
6	0.891	8	0.196	5	19	162
7	0.916	7	0.875	8	2	123
8	0.907	6	0.839	11	18	72
9	0.903	10	0.421	18	14	82
10	0.904	1	0.262	15	17	120
11	0.912	1	0.378	3	1	113
12	0.903	2	0.496	12	6	21
13	0.928	7	0.516	3	2	196
14	0.900	6	0.318	13	20	10
15	0.908	2	0.312	17	20	200
16	0.907	2	0.572	13	2	14
Best	0.928	7	0.516	3	2	196

图11 4个模型的损失函数曲线图

Fig.11 Loss function plots for the four models

图12 4个模型的验证精度曲线图

Fig.12 Validation accuracy plots for the four models

图13 4个机器学习模型的ROC曲线与AUC值

Fig.13 ROC curves and AUC values for the four models

表4 4个集成学习模型的性能比较

Table 4 Comparison of performance for the four models

模型	精度	准确率	召回率	F₁分数	kappa	AUC
RF	0.888	0.900	0.883	0.885	0.773	0.883 2
BO-RF	0.899	0.907	0.897	0.896	0.805	0.891 6
AdaBoost	0.912	0.920	0.906	0.910	0.821	0.906 8
BO-AdaBoost	0.928	0.940	0.923	0.926	0.854	0.962 1

图14 使用RF(a)、BO-RF(b)、AdaBoost(c)和BO-AdaBoost(d)模型预测的Mn的成矿预测图与已知矿点叠加图

Fig.14 Overlay of prediction maps of Mn and known ore points using RF (a), AdaBoost (b), BO-RF (c) and BO-AdaBoost (d) models

表5 4个集成学习模型的预测结果占总面积百分比

Table 5 The percentage of the total area for the four models predictions results

模型	各区域面积占比/%
模型	极低区域	低区域	中等区域	高区域	极高区域
RF	62.13	21.47	6.77	4.88	4.75
BO-RF	63.99	19.16	8.13	4.62	4.10
AdaBoost	69.03	18.47	5.19	4.39	2.93
BO-AdaBoost	72.75	15.26	5.37	4.33	2.29

参考文献 52

[1]	ZHOU Q, WU C L, HU X Y, et al. A new metallogenic model for the giant manganese deposits in northeastern Guizhou, China[J]. Ore Geology Reviews, 2022, 149: 105070.
[2]	吴冲龙, 周琦, 徐凯, 等. 用于大数据预测的大塘坡式锰矿找矿过程复盘研究[J]. 贵州地质, 2022, 39(3): 189-204.
[3]	周琦, 吴冲龙. 基于大数据的智慧探矿模式实验研究与进展[J]. 地学前缘, 2024, 31(6): 350-367. DOI
[4]	吴冲龙, 刘刚. 大数据与地质学的未来发展[J]. 地质通报, 2019, 38(7): 1081-1088.
[5]	曹亚琴, 王永志, 卢鹏羽. 基于机器学习的成矿背景异常分解关键参数的自动计算[J]. 地球物理学进展, 2021, 36(3): 1226-1235.
[6]	PARSA M, CARRANZA E J M. Modulatingthe impacts of stochastic uncertainties linked to deposit locations in data-driven predictive mapping of mineral prospectivity[J]. Natural Resources Research, 2021, 30(5): 3081-3097.
[7]	XU K, ZHAO S, WU C, et al. Manganese mineral prospectivity based on deep convolutional neural networks in Songtao of northeastern Guizhou[J]. Earth Science Informatics, 2024, 17(2): 1681-1697.
[8]	陈国雄, 张越鹏, 罗磊, 等. 数据驱动斑岩型矿床时空预测模型[J]. 地学前缘, 2025, 32(4): 46-59.
[9]	XIAO F, CHEN W, WANG J, et al. A hybrid logistic regression: gene expression programming model and its application to mineral prospectivity mapping[J]. Natural Resources Research, 2022, 31(4): 2041-2064.
[10]	LIU Y, ZHOU K, XIA Q. A MaxEnt model for mineral prospectivity mapping[J]. Natural Resources Research, 2018, 27(3): 299-313.
[11]	ZUO R, CARRANZA E J M. Support vector machine: a tool for mapping mineral prospectivity[J]. Computers & Geosciences, 2011, 37(12): 1967-1975.
[12]	MAEPA F, SMITH R S, TESSEMA A. Support vector machine and artificial neural network modelling of orogenic gold prospectivity mapping in the Swayze greenstone belt, Ontario, Canada[J]. Ore Geology Reviews, 2021, 130: 103968.
[13]	SUN T, CHEN F, ZHONG L X, et al. GIS-based mineral prospectivity mapping using machine learning methods: a case study from Tongling ore district, eastern China[J]. Ore Geology Reviews, 2019, 109: 26-49.
[14]	RODRIGUEZ-GALIANO V, SANCHEZ-CASTILLO M, CHICA-OLMO M, et al. Machine learning predictive models for mineral prospectivity: an evaluation of neural networks, random forest, regression trees and support vector machines[J]. Ore Geology Reviews, 2015, 71: 804-818.
[15]	CARRANZA E J M, LABORTE A G. Data-driven predictive mapping of gold prospectivity, Baguio district, Philippines: application of random forests algorithm[J]. Ore Geology Reviews, 2015, 71: 777-787.
[16]	CHEN M, XIAO F. Projection pursuit random forest for mineral prospectivity mapping[J]. Mathematical Geosciences, 2023, 55(7): 963-987.
[17]	YANG N, ZHANG Z, YANG J, et al. Mineral prospectivity prediction by integration of convolutional autoencoder network and random forest[J]. Natural Resources Research, 2022, 31(3): 1103-1119.
[18]	YANG F, WANG Z, ZUO R, et al. Quantification of uncertainty associated with evidence layers in mineral prospectivity mapping using direct sampling and convolutional neural network[J]. Natural Resources Research, 2023, 32(1): 79-98.
[19]	LI C, XIAO K, SUN L, et al. CNN-Transformers for mineral prospectivity mapping in the Maodeng-Baiyinchagan area, southern Great Xing’an Range[J]. Ore Geology Reviews, 2024, 167: 106007.
[20]	LIU Z, YU S, DENG H, et al. 3D mineral prospectivity modeling in the Sanshandao goldfield, China using the convolutional neural network with attention mechanism[J]. Ore Geology Reviews, 2024, 164: 105861.
[21]	LI T, ZUO R, ZHAO X, et al. Mapping prospectivity for regolith-hosted REE deposits via convolutional neural network with generative adversarial network augmented data[J]. Ore Geology Reviews, 2022, 142: 104693.
[22]	WU Y, LIU B, GAO Y, et al. Mineral prospecting mapping with conditional generative adversarial network augmented data[J]. Ore Geology Reviews, 2023, 163: 105787.
[23]	CHEN Q, CUI Z, LIU G, et al. Deep convolutional generative adversarial networks for modeling complex hydrological structures in Monte-Carlo simulation[J]. Journal of Hydrology, 2022, 610: 127970.
[24]	CAI Y, LI X, ZHANG M, et al. Mapping wetland using the object-based stacked generalization method based on multi-temporal optical and SARdata[J]. International Journal of Applied Earth Observation and Geoinformation, 2020, 92: 102164.
[25]	YIN J, LI N. Ensemble learning models with a Bayesian optimization algorithm for mineral prospectivity mapping[J]. Ore Geology Reviews, 2022, 145: 104916.
[26]	SAGI O, ROKACH L. Ensemble learning: a survey[J]. Wiley Interdisciplinary Reviews: Data Miningand Knowledge Discovery, 2018, 8(4): e1249.
[27]	ROKACH L. Ensemble learning: pattern classification using ensemble methods[M]. Singapore: World Scientific, 2019.
[28]	SHAN W, LI D, LIU S, et al. A random feature mapping method based on the AdaBoost algorithm and results fusion for enhancing classification performance[J]. Expert Systems with Application, 2024, 256: 124902.
[29]	RAO C, LI M, HUANG T, et al. Stroke risk assessment decision-making using a machine learning model: logistic-AdaBoost[J]. Computer Modeling in Engineering & Sciences, 2024, 139(4): 699-724.
[30]	CHANDRAN D, CHITHRA N R. Predictive performance of ensemble learning boosting techniques in daily streamflow simulation[J]. Water Resources Management, 2025, 39(3): 1235-1259.
[31]	ZHAO J, CHI H, SHAO Y, et al. Application of AdaBoost Algorithms in Fe mineral prospectivity prediction: a case study in Hongyuntan-Chilongfeng Mineral district, Xinjiang Province, China[J]. Natural Resources Research, 2022, 31(4): 2001-2022.
[32]	BREIMAN L. Random forests[J]. Machine Learn, 2001, 45(1): 5-32.
[33]	LI Q, CHEN G, WANG D. Mineral prospectivity mapping using semi-supervised machine learning[J]. Mathematical Geosciences, 2025, 57(2): 275-305.
[34]	HARRIS J R, STRONG J, THURSTON P, et al. Mineral prospectivity mapping and differential metal endowment between two greenstone belts in the Canadian superior craton[J]. Natural Resources Research, 2025, 34(1): 97-120.
[35]	REMIDI S, BOUTALEB A, TACHI S E, et al. Ensemble machine learning model for exploration and targeting of Pb-Zn deposits in algeria[J]. Earth Science Informatics, 2025, 18(2): 1-26.
[36]	CHEN Y L, SUI Y H. Dictionary learning for integration of evidential layers for mineral prospectivity modeling[J]. Ore Geology Reviews, 2022, 41: 1-12.
[37]	SHAHRIARI B, SWERSKY K, WANG Z, et al. Taking the human out of the loop: a review of Bayesian optimization[J]. Proceedings of the IEEE, 2015, 104(1): 148-175.
[38]	周琦, 杜远生, 袁良军, 等. 黔湘渝毗邻区南华纪武陵裂谷盆地结构及其对锰矿的控制作用[J]. 地球科学, 2016, 41(2): 177-188.
[39]	YOUSEFI M, KREUZER O P, NYKäNEN V, et al. Exploration information systems-a proposal for the future use of GIS in mineral exploration targeting[J]. Ore Geology Reviews, 2019, 111: 103005.
[40]	ZHANG J M, ZENG Z F, WU Y G, et al. Balanced morphological filters for horizontal boundaries enhancement of the potential field sources[J]. Applied Geophysics, 2024, 21(1): 147-156.
[41]	CHENG Q, AGTERBERG F P. Singularity analysis of ore-mineral and toxic trace elements in stream sediments[J]. Computers & Geosciences, 2009, 35(2): 234-244.
[42]	徐凯, 袁良军, 杨炳南, 等. 黔东北伴生-次生矿物遥感数据组合式挖掘与隐伏锰矿信息提取[J]. 地质科技通报, 2020, 39(4): 37-43.
[43]	YOUSEFI M, CARRANZA E J M, KREUZER O P, et al. Data analysis methods for prospectivity modelling as applied to mineral exploration targeting: state-of-the-art and outlook[J]. Journal of Geochemical Exploration, 2021, 229: 106839.
[44]	FAWCETT T. An introduction to ROC analysis[J]. Pattern Recognition Letters, 2006, 27(8): 861-874.
[45]	CHEN G, HUANG N, Wu G, et al. Mineral prospectivity mapping based on wavelet neural network and Monte Carlo simulations in the Nanling W-Sn metallogenic province[J]. Ore Geology Reviews, 2022, 143: 104765.
[46]	LIN N, CHEN Y, LIU H, et al. A comparative study of machine learning models with hyperparameter optimization algorithm for mapping mineral prospectivity[J]. Minerals, 2021, 11(2): 1-31.
[47]	LEE K, JEONG H O, LEES, et al. CPEM: accurate cancer type classification based on somatic alterations using an ensemble of a random forest and a deep neural network[J]. Scientific Reports, 2019, 9(1): 1-9.
[48]	CHEN J, LI K. Parallel Adaboost with optimized decision trees for high-dimensional data classification[J]. IEEE Transactions on Parallel and Distributed Systems, 2021, 32(6): 1312-1325.
[49]	CARRANZA E J M, HALE M, FAASSEN C. Selection of coherent deposit-type locations and their application in data-driven mineral prospectivity mapping[J]. Ore Geology Reviews, 2008, 33: 536-558.
[50]	LISITSIN V. Spatial data analysis of mineral deposit point patterns: applications to exploration targeting[J]. Ore Geology Reviews, 2015, 71: 861-881.
[51]	WANG J, ZUO R, XIONG Y. Mapping mineral prospectivity via semi-supervised random forest[J]. Natural Resources Research, 2020, 29: 189-202.
[52]	AHNEMAN D T, ESTRADA J G, LIN S, et al. Predicting reaction performance in C-N cross-coupling using machine learning[J]. Science, 2018, 360(6385): 186-190. DOI PMID

基于集成学习模型与贝叶斯优化算法的成矿预测

Metallogenic prediction based on ensemble learning models and Bayesian Optimization Algorithm

RichHTML

PDF (PC)

可视化

摘要/Abstract

引用本文

使用本文

图/表 19

参考文献 52

相关文章 15

编辑推荐

Metrics

本文评价

[1]	邓军, 王长明, 李文昌, 杨立强, 王庆飞. 三江特提斯复合造山与成矿作用研究态势及启示[J]. 地学前缘, 20140101, 21(1): 52-64.
[2]	肖凡, 杨华清, 唐奥, 黄旋财, 王翠翠. 基于机器学习与多源数据融合的东天山戈壁沙漠覆盖区中-酸性侵入岩岩性填图[J]. 地学前缘, 2025, 32(4): 199-212.
[3]	陈国雄, 张越鹏, 罗磊, 夏庆霖, 成秋明. 数据驱动斑岩型矿床时空预测模型[J]. 地学前缘, 2025, 32(4): 46-59.
[4]	李楠, 尹世滔, 柳炳利, 肖克炎, 王成辉, 代鸿章, 宋相龙. 知识-数据联合驱动的可解释智能矿产预测研究:以四川可尔因矿集区为例[J]. 地学前缘, 2025, 32(4): 60-77.
[5]	简富源, 张子鸣, 董岳霖, 张文璟, 郝风云, 王一鸣, 王宇, 张振杰. 基于多重分形与随机森林的新疆哈巴河金矿成矿预测[J]. 地学前缘, 2025, 32(4): 78-94.
[6]	徐凯, 徐城阳, 吴冲龙, 蔡婧云, 孔春芳. 基于样本扩充的黔西北垭都-蟒硐矿区铅锌矿成矿预测研究[J]. 地学前缘, 2025, 32(4): 95-107.
[7]	黄继先, 李苇琪, 邓浩, 万世军, 李晓, 毛先成. 基于勘查大数据的控矿作用空间非平稳性定量研究:以三山岛金矿床为例[J]. 地学前缘, 2025, 32(4): 317-328.
[8]	徐东辉, 黎涛, 林艳竹, 陈添斐. 基于关联性监测指标的辽东湾地下水硝酸盐源解析[J]. 地学前缘, 2025, 32(4): 376-387.
[9]	袁峰, 李晓晖, 田卫东, 周官群, 汪金菊, 葛粲, 国显正, 郑超杰. 三维成矿预测关键问题[J]. 地学前缘, 2024, 31(4): 119-128.
[10]	张前龙, 周永章, 郭兰萱, 原桂强, 虞鹏鹏, 王汉雨, 朱彪彪, 韩枫, 龙师尧. 找矿知识图谱的智能化应用:以钦杭成矿带斑岩铜矿为例[J]. 地学前缘, 2024, 31(4): 7-15.
[11]	王琳, 季晓慧, 杨眉, 何明跃, 张招崇, 曾姗, 王玉柱. 基于数据增强和集成学习的矿物图像识别[J]. 地学前缘, 2024, 31(4): 87-94.
[12]	付宇, 曹文庚, 张春菊, 翟文华, 任宇, 南天, 李泽岩. 基于集成学习优化的河套盆地地下水砷风险评估[J]. 地学前缘, 2024, 31(3): 371-380.
[13]	谷浩, 杨泽强, 高猛, 唐相伟, 王东晓, 刘奎松, 杨树人, 郭跃闪, 王云, 王功文. 河南围山城金银矿集区三维地质建模与成矿预测[J]. 地学前缘, 2024, 31(3): 245-259.
[14]	刘奇鑫, 顾行发, 王春梅, 杨健, 占玉林. 不同尺度的土壤含水量主被动微波联合反演方法研究[J]. 地学前缘, 2024, 31(2): 42-53.
[15]	胡义明, 陈腾, 罗序义, 唐超, 梁忠民. 基于机器学习模型的淮河流域中长期径流预报研究[J]. 地学前缘, 2022, 29(3): 284-291.