

地学前缘 ›› 2025, Vol. 32 ›› Issue (4): 182-198.DOI: 10.13745/j.esf.sf.2025.4.72
叶舒婉1( ), 侯卫生1,2,*(
), 侯卫生1,2,*( ), 杨玠3, 汪海城4, 白芸4, 王永志5
), 杨玠3, 汪海城4, 白芸4, 王永志5
收稿日期:2025-02-20
修回日期:2025-05-10
出版日期:2025-07-25
发布日期:2025-08-04
通信作者:
*侯卫生(1976—),男,教授,博士生导师,主要从事三维地质建模和全波形反演研究。E-mail: houwsh@mail.sysu.edu.cn
作者简介:叶舒婉(1998—),女,博士研究生,主要从事三维地质建模研究。E-mail: yeshw6@mail2.sysu.edu.cn
基金资助:
YE Shuwan1( ), HOU Weisheng1,2,*(
), HOU Weisheng1,2,*( ), YANG Jie3, WANG Haicheng4, BAI Yun4, WANG Yongzhi5
), YANG Jie3, WANG Haicheng4, BAI Yun4, WANG Yongzhi5
Received:2025-02-20
Revised:2025-05-10
Online:2025-07-25
Published:2025-08-04
摘要:
高精度的三维地质建模是数字孪生技术快速发展的重要基础,为资源预测、工程规划和灾害防治等领域提供了关键支撑。传统三维地质建模方法多依靠人工交互,难以满足复杂地质环境下对精细结构表达和实时更新的需求。为突破这些局限,近年来引入的机器学习与深度学习为地质建模提供了新的智能化解决方案,有效提升了模型的自动化程度和复杂结构的表达能力。本文系统回顾了三维地质建模的发展历程,总结了半智能化、机器学习和深度学习三个发展阶段的技术特征;深入剖析了深度学习与不确定性分析、迁移学习、主成分分析及多点地质统计学等方法的融合方法。同时,针对现有方法在数据稀疏处理、计算复杂性、模型可解释性和实时更新能力方面存在的不足,提出未来的研究趋势与发展方向,包括多模态数据融合、地质知识嵌入、轻量化模型优化、不确定性量化和人工智能大语言模型等。随着智能化建模技术的不断进步,三维地质模型的精度、可靠性和适应性将持续提升,进一步推动地质领域的数字孪生技术应用与工程实践发展。
中图分类号:
叶舒婉, 侯卫生, 杨玠, 汪海城, 白芸, 王永志. 三维地质智能建模研究进展[J]. 地学前缘, 2025, 32(4): 182-198.
YE Shuwan, HOU Weisheng, YANG Jie, WANG Haicheng, BAI Yun, WANG Yongzhi. Advance of 3D smart geological modeling[J]. Earth Science Frontiers, 2025, 32(4): 182-198.

图2 基于TIN-GTP模型的内蒙古桌子山煤田棋盘井煤矿的三维建模结果(据文献[21])
Fig.2 3D modeling result of the Qipanjing coal mine in the Zhuozishan coalfield, Inner Mongolia, based on the TIN-GTP model. Adapted from [21].
| 分类 | 插值方法 | 描述 | 优点 | 缺点 |
|---|---|---|---|---|
| 确定性 插值 | 反距离权重插值 | 基于已知点到未知点的距离加权计算属性值,邻近点影响大 | 简单高效,适合小规模数据 | 忽略空间方向性和自相关性,易过渡平滑 |
| 多样条插值 | 采用分段多项式函数拟合数据,并保持边界连续性 | 适用于连续分布数据,光滑性好,适应复杂边界 | 不适合非平稳数据,计算量大 | |
| 径向基函数插值 | 采用多维曲面拟合,构造最优插值函数,确保插值结果平滑 | 适用于非均匀分布数据,空间连续性强 | 对参数选择敏感,计算复杂 | |
| 离散光滑插值 | 通过最小化误差和光滑度调整插值值,保证整体平滑性和空间一致性 | 插值结果光滑且连续,可处理不规则几何形态 | 计算复杂度高,高异质性区域难以捕捉局部特征 | |
| 统计插值 | 克里金插值 | 基于变异函数描述空间自相关性,进行最优线性无偏估计 | 考虑空间结构,支持误差估计 | 计算复杂,参数选择依赖用户经验;在大规模数据计算时计算量大 |
表1 常用插值方法
Table 1 Interpolation methods used in 3D geological modeling
| 分类 | 插值方法 | 描述 | 优点 | 缺点 |
|---|---|---|---|---|
| 确定性 插值 | 反距离权重插值 | 基于已知点到未知点的距离加权计算属性值,邻近点影响大 | 简单高效,适合小规模数据 | 忽略空间方向性和自相关性,易过渡平滑 |
| 多样条插值 | 采用分段多项式函数拟合数据,并保持边界连续性 | 适用于连续分布数据,光滑性好,适应复杂边界 | 不适合非平稳数据,计算量大 | |
| 径向基函数插值 | 采用多维曲面拟合,构造最优插值函数,确保插值结果平滑 | 适用于非均匀分布数据,空间连续性强 | 对参数选择敏感,计算复杂 | |
| 离散光滑插值 | 通过最小化误差和光滑度调整插值值,保证整体平滑性和空间一致性 | 插值结果光滑且连续,可处理不规则几何形态 | 计算复杂度高,高异质性区域难以捕捉局部特征 | |
| 统计插值 | 克里金插值 | 基于变异函数描述空间自相关性,进行最优线性无偏估计 | 考虑空间结构,支持误差估计 | 计算复杂,参数选择依赖用户经验;在大规模数据计算时计算量大 |
| 常见分类器 | 描述 | 优点 | 缺点 |
|---|---|---|---|
| 朴素贝叶斯 | 基于贝叶斯定理,假设特征条件独立,用于地质单元分类和初步建模 | 计算高效,参数简单,适合小样本数据 | 泛化能力弱,不适用于连续数据,对特征分布依赖性强 |
| BP神经网络 | 基于多层前馈神经网络,建模非线性地质特征,适用于预测与分类任务 | 非线性拟合强,结构灵活 | 训练慢,参数敏感,易过拟合,计算效率低 |
| 随机森林 | 多决策树集成,适用于复杂地质属性建模和多源数据整合 | 非线性建模能力强,抗噪性好,可并行计算 | 模型复杂,超参数敏感,资源消耗大 |
| XGBoost | 基于梯度提升决策树,适用于处理复杂地质数据的非线性特征和稀疏性问题 | 计算高效,非线性建模能力强,适用于多源异构数据 | 参数调优困难,可解释性较低 |
| 支持向量机 | 通过核函数将数据映射到高维空间,实现地层预测和结构分割 | 适用于高维小样本,核函数灵活,鲁棒性和泛化强 | 计算复杂,参数调优困难,对不平衡数据敏感 |
表2 常见分类器的描述
Table 2 Description of classifiers usually used in 3D geological modeling
| 常见分类器 | 描述 | 优点 | 缺点 |
|---|---|---|---|
| 朴素贝叶斯 | 基于贝叶斯定理,假设特征条件独立,用于地质单元分类和初步建模 | 计算高效,参数简单,适合小样本数据 | 泛化能力弱,不适用于连续数据,对特征分布依赖性强 |
| BP神经网络 | 基于多层前馈神经网络,建模非线性地质特征,适用于预测与分类任务 | 非线性拟合强,结构灵活 | 训练慢,参数敏感,易过拟合,计算效率低 |
| 随机森林 | 多决策树集成,适用于复杂地质属性建模和多源数据整合 | 非线性建模能力强,抗噪性好,可并行计算 | 模型复杂,超参数敏感,资源消耗大 |
| XGBoost | 基于梯度提升决策树,适用于处理复杂地质数据的非线性特征和稀疏性问题 | 计算高效,非线性建模能力强,适用于多源异构数据 | 参数调优困难,可解释性较低 |
| 支持向量机 | 通过核函数将数据映射到高维空间,实现地层预测和结构分割 | 适用于高维小样本,核函数灵活,鲁棒性和泛化强 | 计算复杂,参数调优困难,对不平衡数据敏感 |

图6 基于Extended-GOSIM的三维建模结果(据文献[52])
Fig.6 Three-dimensional geological modeling result constructed using the Extended-GOSIM algorithm. Adapted from [52].
| 分类方法 | 类型 | 描述 | 优点 | 缺点 |
|---|---|---|---|---|
| 核心思想 | 图像学 方法 | 以移动模板方式从训练图像提取空间模式,并粘贴至模拟网格,实现模型重构(如ANSIM、DISPAT、GOSIM等) | 模板可调,直观表达局部模式 | 小模板丢失宏观特征,大模板降低随机性 |
| 数据事件 方法 | 依据待模拟点的概率分布函数进行随机模拟,从已知数据提取统计特征(如SNESIM、IMPALA、HOSIM等) | 自动化高,适应复杂建模条件 | 难捕捉隐藏隐含特征,依赖数据驱动 | |
| 模拟过程 | 序贯模拟 方法 | 按预设路径逐点赋值,仅遍历网格一次(如SNESIM、SIMPAT、DS、HOSIM、CCSIM等) | 模拟效率高,方法简单,易实现 | 误差逐步累积,难以捕捉复杂全局特征 |
| 迭代过程 方法 | 以初始模型为基础,反复优化属性值,直至满足损失函数阈值或迭代条件(如GOSIM、PCTO-SIM等) | 误差少,精度高,保留更多已知信息 | 依赖初始模型,计算成本高 |
表3 常用基于MPS的三维地质建模方法对比
Table 3 Comparison of MPS-based methods for modeling 3D geological structures
| 分类方法 | 类型 | 描述 | 优点 | 缺点 |
|---|---|---|---|---|
| 核心思想 | 图像学 方法 | 以移动模板方式从训练图像提取空间模式,并粘贴至模拟网格,实现模型重构(如ANSIM、DISPAT、GOSIM等) | 模板可调,直观表达局部模式 | 小模板丢失宏观特征,大模板降低随机性 |
| 数据事件 方法 | 依据待模拟点的概率分布函数进行随机模拟,从已知数据提取统计特征(如SNESIM、IMPALA、HOSIM等) | 自动化高,适应复杂建模条件 | 难捕捉隐藏隐含特征,依赖数据驱动 | |
| 模拟过程 | 序贯模拟 方法 | 按预设路径逐点赋值,仅遍历网格一次(如SNESIM、SIMPAT、DS、HOSIM、CCSIM等) | 模拟效率高,方法简单,易实现 | 误差逐步累积,难以捕捉复杂全局特征 |
| 迭代过程 方法 | 以初始模型为基础,反复优化属性值,直至满足损失函数阈值或迭代条件(如GOSIM、PCTO-SIM等) | 误差少,精度高,保留更多已知信息 | 依赖初始模型,计算成本高 |

图9 基于3D CNN模型的黑龙江青年甸地区三维建模结果(a)和相应的剖面图(b)(据文献[55])
Fig.9 3D lithostratigraphic modeling result based on the 3D CNN model (a) and the corresponding cross-sectional view (b). Adapted from [55].
| 类别 | 方法 | 优点 | 缺点 | 适用场景 |
|---|---|---|---|---|
| 无条件建模 | 传统GAN方法 | 简单直接,可捕捉整体地质模式;再现多样性高的地质模式 | 模式崩塌风险大,高分辨率建模细节不足 | 简单地质分布建模 |
| 渐进式GAN方法 | 逐层训练,适配高分辨率,细节更清晰 | 训练复杂,需高算力 | 多尺度地质建模,高分辨率地质建模 | |
| 有条件建模 | 模拟器输入向量搜寻的条件化方法 | 适合多约束条件,可结合梯度下降和MCMC(Markov Chain Monte Carlo)优化 | 条件变动需重新搜索,计算开销大 | 精确井控建模,数据稀疏场景 |
| 模拟器直接条件化方法 | 条件数据直接输入,操作便捷,建模效率高 | 模型结构复杂,对间接条件数据适应性差 | 快速建模,适用于复杂多源约束 |
表4 基于GAN的建模方法分类对比表
Table 4 Comparison of GAN-based modeling methods
| 类别 | 方法 | 优点 | 缺点 | 适用场景 |
|---|---|---|---|---|
| 无条件建模 | 传统GAN方法 | 简单直接,可捕捉整体地质模式;再现多样性高的地质模式 | 模式崩塌风险大,高分辨率建模细节不足 | 简单地质分布建模 |
| 渐进式GAN方法 | 逐层训练,适配高分辨率,细节更清晰 | 训练复杂,需高算力 | 多尺度地质建模,高分辨率地质建模 | |
| 有条件建模 | 模拟器输入向量搜寻的条件化方法 | 适合多约束条件,可结合梯度下降和MCMC(Markov Chain Monte Carlo)优化 | 条件变动需重新搜索,计算开销大 | 精确井控建模,数据稀疏场景 |
| 模拟器直接条件化方法 | 条件数据直接输入,操作便捷,建模效率高 | 模型结构复杂,对间接条件数据适应性差 | 快速建模,适用于复杂多源约束 |
| 方法 | 仅采用深度学习的方法 | 融合不确定分析和深度学习的方法 |
|---|---|---|
| 模型输出 | 单一确定性结果 | 输出预测结果及其置信度和不确定度 |
| 预测可信度表达 | 可通过后验概率或准确率等间接评估,但存在过度置信问题 | 量化每一预测的置信度和不确定度,能区分高可信与低可信预测 |
| 结果表达能力 | 难以判断模型在非平稳或异常区域的可信程度 | 根据不确定度识别模型效果,增强对地质异常区域的响应能力 |
| 对抗鲁棒性 | 易被扰动误导,错误预测置信度高 | 错误预测伴随高不确定度,增强安全性和鲁棒性 |
| 计算复杂度 | 较低 | 较高 |
| 适用环境 | 数据充足、结构清晰、分类明确的地质环境 | 数据稀缺、存在噪声或结构复杂的地质场景 |
表5 仅采用深度学习的三维地质重建方法与融合不确定性分析的深度学习方法对比表
Table 5 Comparison between deep learning-based 3D geological reconstruction and the approach integrating uncertainty analysis
| 方法 | 仅采用深度学习的方法 | 融合不确定分析和深度学习的方法 |
|---|---|---|
| 模型输出 | 单一确定性结果 | 输出预测结果及其置信度和不确定度 |
| 预测可信度表达 | 可通过后验概率或准确率等间接评估,但存在过度置信问题 | 量化每一预测的置信度和不确定度,能区分高可信与低可信预测 |
| 结果表达能力 | 难以判断模型在非平稳或异常区域的可信程度 | 根据不确定度识别模型效果,增强对地质异常区域的响应能力 |
| 对抗鲁棒性 | 易被扰动误导,错误预测置信度高 | 错误预测伴随高不确定度,增强安全性和鲁棒性 |
| 计算复杂度 | 较低 | 较高 |
| 适用环境 | 数据充足、结构清晰、分类明确的地质环境 | 数据稀缺、存在噪声或结构复杂的地质场景 |
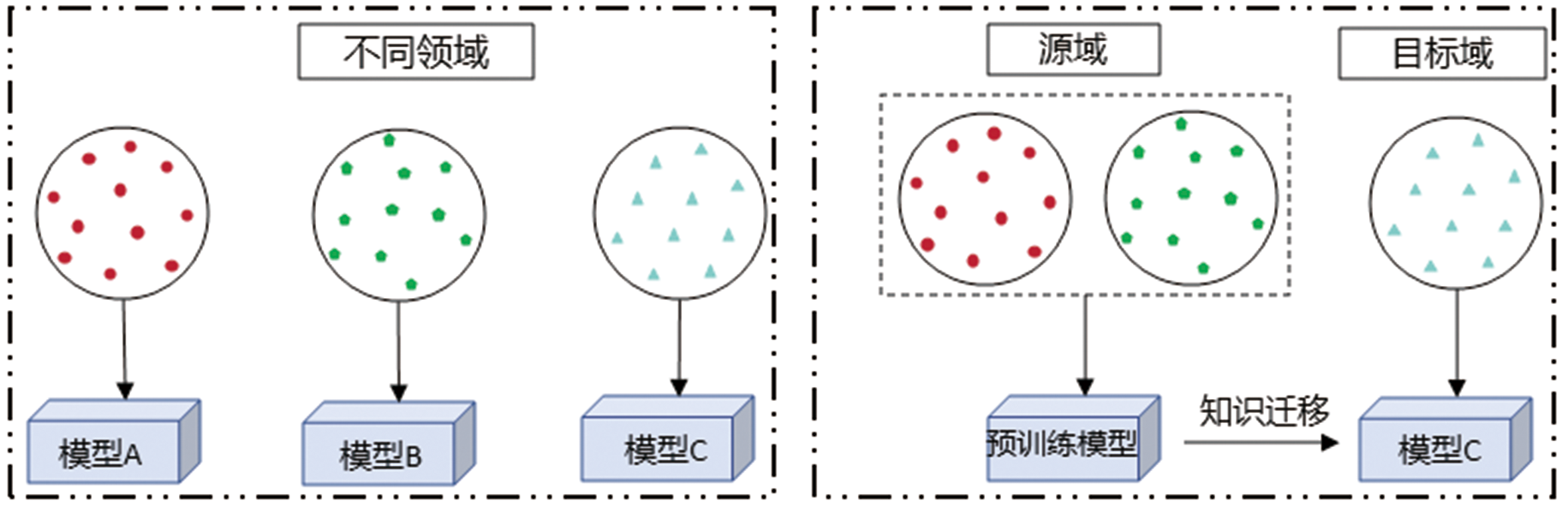
图12 传统机器学习(左)与迁移学习(右)比较(据文献[79-80])
Fig.12 Comparison between conventional machine learning (left) and transfer learning (right). Adapted from [79-80].
| [1] | GROSHEV M, GUIMARÃES C, MARTÍN-PÉREZ J, et al. Toward intelligent cyber-physical systems: digital twin meets artificial intelligence[J]. IEEE Communications Magazine, 2021, 59(8): 14-20. |
| [2] | AIDAN F, HONG F, CHARLES D, et al. Digital twin: enabling technologies, challenges and open research[J]. IEEE Access, 2020, 8: 108952-108971. |
| [3] | LIU G P. Control strategies for digital twin systems[J]. IEEE/CAA Journal of Automatica Sinica, 2024, 11(1): 170-180. |
| [4] |
李三忠, 索艳慧, 戴黎明, 等. 元地球与数字孪生: 思想突破、 技术变革与范式转换[J]. 地学前缘, 2024, 31(1): 46-63.
DOI |
| [5] | 齐天泓, 黄海峰, 曹乐, 等. 智能制造数字孪生概念模型与关键技术研究[J]. 信息技术与标准化, 2024, 11: 45-50, 60. |
| [6] | 张颖伟, 高鸿瑞, 张鼎森, 等. 基于多智能体的数字孪生及其在工业中应用的综述[J]. 控制与决策, 2023, 38(8): 2168-2182. |
| [7] | MIN Q F, LU Y G, LIU Z Y, et al. Machine learning based digital twin framework for production optimization in petrochemical Industry[J]. International Journal of Information Management, 2019, 49: 502-519. |
| [8] |
刘文岭, 韩大匡. 数字孪生油气藏: 智慧油气田建设的新方向[J]. 石油学报, 2022, 43(10): 1450-1461.
DOI |
| [9] | HOULDING S W. 3D Geoscience modeling: computer techniques for geological characterization[M]. Berlin: Springer-Verlag, 1994: 85-90. |
| [10] | GUO J T, WU L X, ZHOU W H, et al. Towards automatic and topologically consistent 3D regional geological modeling from boundaries and attitudes[J]. Isprs International Journal of Geo-Information, 2016, 5 (2): 17. |
| [11] | SHINDE PP, SHAH S. A review of machine learning and deep learning applications[C]// 2018 Fourth International Conference on Computing Communication Control and Automation(ICCUBEA). IEEE, 2018: 1-6. |
| [66] | 刘艳鹏, 朱立新, 周永章. 卷积神经网络及其在矿床找矿预测中的应用: 以安徽省兆吉口铅锌矿床为例[J]. 岩石学报, 2018, 34(11): 3217-3224. |
| [67] | LYU B, WANG Y, SHI C. Multi-scale generative adversarial networks (GAN) for generation of three-dimensional subsurface geological models from limited boreholes and prior geological knowledge[J]. Computers and Geotechnics, 2024, 170: 106336. |
| [68] | YANG Z X, CHEN Q Y, CUI Z S, et al. Automatic reconstruction method of 3D geological models based on deep convolutional generative adversarial networks[J]. Computational Geosciences, 2022, 26 (5): 1135-1150. |
| [69] | XIE P F, HOU J G, YIN Y S, et al. Seismic inverse modeling method based on generative adversarial networks[J]. Journal of Petroleum Science and Engineering, 2022, 215: 110652. |
| [70] | LALOY E, HÉRAULT R, JACQUES D, et al. Training-image based geostatistical inversion using a spatial generative adversarial neural network[J]. Water Resources Research, 2018, 54(1): 381-406. |
| [71] | DUPONT E, ZHANG T F, TILKE P, et al. Generating realistic geology conditioned on physical measurements with generative adversarial networks[J]. Statistics, 2018. DOI: 10.48550/arXiv.1802.03065. |
| [72] | ZHANG T F, TILKE P, DUPONT E, et al. Generating geologically realistic 3D reservoir facies models using deep learning of sedimentary architecture with generative adversarial networks[J]. Petroleum Science, 2019, 16 (3): 541-549. |
| [73] | SONG S H, MUKERJI T, HOU J G. GANSim: conditional facies simulation using an improved progressive growing of generative adversarial networks (GANs)[J]. Mathematical Geosciences, 2021, 53(7): 1413-1444. |
| [74] | GOOVAERTS P. Geostatistics for natural resources evaluation[M]. Oxford: Oxford University Press, 1997. |
| [75] | FAN W Y, LIU G, CHEN Q Y, et al. Automatic reconstruction of geological reservoir models based on conditioning data constraints and BicycleGAN[J]. Geoenergy Science and Engineering, 2024, 234: 212690. |
| [76] | KIM S E, YOON H, LEE J. Fast and scalable earth texture synthesis using spatially assembled generative adversarial neural networks[J]. Journal of Contaminant Hydrology, 2021, 243: 103867. |
| [12] | 王新苗. 智能开采工作面精细地质建模研究: 以黄陵某工作面为例[D]. 北京: 煤炭科学研究总院, 2021. |
| [13] | 邹艳红, 何建春. 移动立方体算法的地质体三维空间形态模拟[J]. 测绘学报, 2012, 41(6): 910-917. |
| [14] | 张宝一, 杨莉, 陈笑扬, 等. 基于图切地质剖面的区域成矿地质体三维建模与资源评价: 以桂西南地区锰矿为例[J]. 吉林大学学报(地球科学版), 2017, 47(3): 933-948. |
| [15] | 朱良峰, 潘信. 河流侵淤作用下三维地层模型的构建[J]. 岩土力学, 2005(增刊1): 65-68. |
| [16] | ZHANG H, XU Y. 3D Model Constructing and Dynamic Display of Uncontinuous Geological Entity Based on TIN[J]. Journal of China University of Mining & Technology, 2002, 31 (2): 142-145. |
| [17] | WU L X. Topological relations embodied in a generalized tri-prism (GTP) model for a 3D geoscience modeling system[J]. Computers & Geosciences, 2004, 30 (4): 405-418. |
| [18] | WU S M, WANG Y K, SONG J W, et al. Research on technology of building three-dimensional geological simulation model by octree algorithm Method[C]// International Conference on Mechanical, Material Engineering (MME 2013). 2013: 591-594. |
| [19] | YUAN J, LIU G W, CHAI S L. 3D geological fine modeling and dynamic updating method of fault slope in open-pit coal mine[J]. Scientific Reports, 2024, 14 (1): 29906. |
| [20] | HE L, ZHANG J R, CHEN S Z, et al. Three dimensional hydrogeological modeling method and application based on TINGTPTEN[J]. Earth Science Informatics, 2022, 15 (1): 337-350. |
| [21] | 王晓辉, 刘再斌, 张东亮, 等. 基于TIN-GTP算法的煤矿三维地质建模技术研究[J]. 煤田地质与勘探, 2024, 52(9): 41-48. |
| [22] |
薛涛, 包训栓, 朱小弟, 等. 多源数据三维地质结构模型约束的属性建模方法: 以北京市通州城市副中心为例[J]. 地学前缘, 2023, 30(3): 529-536.
DOI |
| [77] | MOSEGAARD K, TARANTOLA A. Monte Carlo sampling of solutions to inverse problems[J]. Journal of Geophysical Research, 1995, 100 (B7): 12431-12447. |
| [78] | HUANG J X, DENG H, CHEN J, et al. Assessing geometrical uncertainties in geological interface models using Markov chain Monte Carlo sampling via abstract graph[J]. Tectonophysics, 2023, 864: 230032. |
| [79] | PAN S J, YANG Q. Asurvey on transfer learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2010, 22(10): 1345-1359. |
| [80] | 林秋怡, 左仁广. 迁移学习及其在固体地球科学中的应用[J]. 地质科技通报, 2025, 44(1): 346-356. |
| [81] | LONG M, CAO Y, WANG J, et al. Learning transferable features with deep adaptation networks[C]// 32nd International Conference on Machine Learning. 2015: 97-105. |
| [82] |
陈杰, 张挺, 杜奕. 基于自适应深度迁移学习的多孔介质重构[J]. 计算机应用, 2020, 40(4): 1231-1236.
DOI |
| [83] | 芦凤明, 孟瑞刚, 张军华, 等. UNet++和迁移学习相结合的复杂断裂识别方法研究[J]. 地球物理学进展, 2022, 37(3): 1100-1111. |
| [84] |
李小波, 李欣, 闫林, 等. 采用带注意力机制3D U-Net网络的地质模型参数化技术[J]. 石油勘探与开发, 2023, 50(1): 167-173.
DOI |
| [85] | LIU Y, DURLOFSKY L J. 3D CNN-PCA:a deep-learning-based parameterization for complex geomodels[J]. Computers Geosciences, 2021, 148: 104676. |
| [86] | YANG J, LU R, TAO W, et al. MultiURNet for 3D seismic fault attributes fusion detection combined with PCA[J]. Journal of Applied Geophysics, 2024, 221: 105296. |
| [87] | LALOY E, HÉRAULT R, LEE J, et al. Inversion using a new low-dimensional representation of complex binary geological media based on a deep neural network[J]. Advances in Water Resources, 2017, 110: 387-405. |
| [23] | 邢延涛, 李利军. 三维地质体重构中空间数据插值方法的研究[J]. 计算机与数字工程, 2006, 34(12): 45-47. |
| [24] | SHAHBEIK S, AFZAL P, MOAREFVAND P, et al. Comparison between ordinary kriging (OK) and inverse distance weighted (IDW) based on estimation error. Case study: Dardevey iron ore deposit, NE Iran[J]. Arabian Journal of Geosciences, 2014, 7 (9): 3693-3704. |
| [25] | LASLETT G M. Kriging and splines: an empirical comparison of their predictive performance in some applications[J]. Journal of the American Statistical Association, 1994, 89(426): 391-400. |
| [26] | 田宜平, 袁艳斌, 李绍虎, 等. 建立盆地三维构造-地层格架的插值方法[J]. 地球科学, 2000(2): 191-194. |
| [27] | HARDY R L. Multiquadric equations of topography and other irregular surfaces[J]. Journal of Geophysical Research, 1971, 76 (8): 1905-1915. |
| [28] | 高琼, 刘丹丹, 张伟, 等. 一种基于径向基隐式曲面的地质三维建模方法[J]. 测绘与空间地理信息, 2024, 47(7): 183-186. |
| [29] | MALLET J L. Geomodeling[M]. Oxford: Oxford University Press, 2002: 1-599. |
| [30] | MALLET J L. Discrete smooth interpolation[J]. ACM Transactions on Graphics, 1989, 8 (2): 121-144. |
| [31] | DAVIS J C, SAMPSON R J. Statistics and data analysis in geology[M]. New York: John Wiley & Sons, 1986: 238-239. |
| [32] | JIN X, WANG G W, TANG P, et al. 3D geological modelling and uncertainty analysis for 3D targeting in Shanggong gold deposit (China)[J]. Journal of Geochemical Exploration, 2020, 210: 106442. |
| [33] | 唐丙寅, 吴冲龙, 李新川, 等. 一种基于钻孔地质数据的快速递进三维地质建模方法[J]. 岩土力学, 2015, 36(12): 3633-3638. |
| [34] | LI H, NI H Z, FU J M, et al. A domain-decomposition-based parallel approach for 3D geological modeling using radial basis functions interpolation on GPUs[J]. Earth Science Informatics, 2025, 18 (1): 1-16. |
| [35] | TORRES C E, BARBA L A. Fast radial basis function interpolation with Gaussians by localization and iteration[J]. Journal of Computational Physics, 2009, 228 (14): 4976-4999. |
| [36] | WANG X L, GUO J T, FU S H, et al. Towards automatic and rapid 3D geological modelling of urban sedimentary strata from a large amount of borehole data using a parallel solution of implicit equations[J]. Earth Science Informatics, 2024, 17 (1): 421-440. |
| [37] | RISH I. An empirical study of the naive Bayes classifier[C]// IJCAI 2001 workshop on empirical methods in artificial intelligence. 2001: 41-46. |
| [38] | CORTES C, VAPNIK V. Support-vector networks[J]. Machine Learning, 1995, 20 (3): 273-297. |
| [39] | 熊玖琦, 刘星. 基于支持向量机的顾北煤矿北一矿区三维地质模型构建[J]. 科学技术与工程, 2022, 22(19): 8194-8199. |
| [40] | BREIMAN L. Random forests[J]. Machine Learning, 2001, 45 (1): 5-32. |
| [41] | CHEN T Q, GUESTRIN C, ASSOC COMP M. XGBoost: a scalable tree boosting system[C]// 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD). 2016: 785-794. |
| [42] | FU G M, LU Q T, YAN J Y, et al. 3D mineral prospectivity modeling based on machine learning: a case study of the Zhuxi tungsten deposit in northeastern Jiangxi Province, South China[J]. Ore Geology Reviews, 2021, 131: 104010. |
| [43] |
郭甲腾, 刘寅贺, 韩英夫, 等. 基于机器学习的钻孔数据隐式三维地质建模方法[J]. 东北大学学报(自然科学版), 2019, 40(9):1337-1342.
DOI |
| [44] | MARIETHOZ G, RENARD P, STRAUBHAAR J. The direct sampling method to perform multiple-point geostatistical simulations[J]. Water Resources Research, 2010, 46: W11536. |
| [88] | AVALOS S, ORTIZ J M. Recursive convolutional neural networks in a multiple-point statistics framework[J]. Computers & Geosciences, 2020, 141: 104522. |
| [89] | HOU W S, CHEN Y H, LIU H G, et al. Reconstructing three-dimensional geological structures by the multiple-point statistics method coupled with a deep neural network: a case study of a metro station in Guangzhou, China[J]. Tunnelling and Underground Space Technology, 2023, 136: 105089. |
| [90] | HOU W S, LI Y H, YE S W, et al. Mapping 3D overthrust structures by a hybrid modeling method[J]. Earth and Space Science, 2025, 12 (1): e2024EA003916. |
| [91] | 安文通, 廖远琴, 杨其菠, 等. 地下空间多元数据融合与可视化关键技术研究[J/OL]. 地学前缘, 2024: 1-13[2025-01-10]. https://doi.org/10.13745/j.esf.sf.2024.11.61. |
| [92] | 邱芹军, 田苗, 吴麒瑞, 等. 基于多源异构数据的地质知识图谱构建与应用[J/OL]. 地学前缘, 2024: 1-17[2025-01-11]. https://doi.org/10.13745/j.esf.sf.2024.11.69. |
| [93] | ZHANG Y F, WANG Z Y, HE Z T, et al. BB-GeoGPT: a framework for learning a large language model for geographic information science[J]. Information Processing & Management, 2024, 61(5): 103808. |
| [94] | ZHANG Y F, WEI C, HE Z T, et al. GeoGPT: An assistant for understanding and processing geospatial tasks[J]. International Journal of Applied Earth Observation and Geoinformation, 2024, 131: 103976. |
| [45] | GUARDIANO F B, SRIVASTAVA R M. Multivariate geostatistics: beyond bivariate moments[M]// SOARES A. Geostatistics Tróia ’92. Dordrecht: Springer, 1993: 133-147. |
| [46] | STREBELLE S. Conditional simulation of complex geological structures using multiple-point statistics[J]. Mathematical Geology, 2002, 34 (1): 1-21. |
| [47] | ARPAT G B. Sequential simulation with patterns[M]. Stanford: Stanford University, 2005. |
| [48] | DIMITRAKOPOULOS R, MUSTAPHA H, GLOAGUEN E. High-order statistics of spatial random fields: exploring spatial cumulants for modeling complex non-gaussian and non-linear phenomena[J]. Mathematical Geosciences, 2010, 42 (1): 65-99. |
| [49] | TAHMASEBI P, SAHIMI M, CAERS J. MS-CCSIM: accelerating pattern-based geostatistical simulation of categorical variables using a multi-scale search in Fourier space[J]. Computers & Geosciences, 2014, 67: 75-88. |
| [50] | YANG L, HOU W S, CUI C J, et al. GOSIM:a multi-scale iterative multiple-point statistics algorithm with global optimization[J]. Computers & Geosciences, 2016, 89: 57-70. |
| [51] | POURFARD M, ABDOLLAHIFARD M J, FAEZ K, et al. PCTO-SIM: multiple-point geostatistical modeling using parallel conditional texture optimization[J]. Computers & Geosciences, 2017, 102: 116-138. |
| [52] | HOU W S, LIU H G, ZHENG T C, et al. Extended GOSIM: MPS-driven simulation of 3D geological structure using 2D cross-sections[J]. Earth and Space Science, 2022, 9(6): e2021EA001801. |
| [53] | MINAR M R, NAHER J. Recent advances in deep learning: an overview[J]. Computer Science, 2018. DOI: 10.13140/RG.2.2.24831.10403. |
| [54] | LI T, ZUO R G, XIONG Y H, et al. Random-drop data augmentation of deep convolutional neural network for mineral prospectivity mapping[J]. Natural Resources Research, 2021, 30(1): 27-38. |
| [55] | ZHANG B Y, XU Z H, WEI X Z, et al. Deep subsurface pseudo-lithostratigraphic modeling based on three-dimensional convolutional neural network (3D CNN) using inversed geophysical properties and shallow subsurface geological model[J]. Lithosphere, 2024, 2024 (1): lithosphere_2023_2273. |
| [56] | GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[C]// 28th Conference on Neural Information Processing Systems (NIPS). 2014: 2672-2680. |
| [57] | KINGMA D P, WELLING M. Anintroduction to variational autoencoders[J]. Foundations and Trends in Machine Learning, 2019, 12(4): 4-89. |
| [58] | HILLIER M, WELLMANN F, BRODARIC B, et al. Three-dimensional structural geological modeling using graph neural networks[J]. Mathematical Geosciences, 2021, 53 (8): 1725-1749. |
| [59] | ZHOU C Y, OUYANG J W, MING W H, et al. A stratigraphic prediction method based on machine learning[J]. Applied Sciences-Basel, 2019, 9 (17): 3553. |
| [60] |
柳林, 孙毅, 李万武. 基于CNN海上钻井平台检测模型的构建及训练算法分析[J]. 测绘通报, 2022, (7): 26-32, 99.
DOI |
| [61] | SRIVASTAVA N, HINTON G, KRIZHEVSKY A, et al. Dropout: a simple way to prevent neural networks from overfitting[J]. The Journal of Machine Learning Research, 2014, 15 (1): 1929-1958. |
| [62] | HE M M, ZHANG Z Q, REN J, et al. Deep convolutional neural network for fast determination of the rock strength parameters using drilling data[J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 123: 104084. |
| [63] | 'AVALOS S A, ORTIZ J A M. Geological modeling using a recursive convolutional neural networks approach[J]. Electrical Engineering and Systems Science, 2019. DOI: 10.48550/arXiv.1904.12190. |
| [64] | RAN X J, XUE L F, ZHANG Y Y, et al. Rock classification from field image patches analyzed using a deep convolutional neural network[J]. Mathematics, 2019, 7 (8): 755. |
| [65] | SANG X J, XUE L F, RAN X J, et al. Intelligent high-resolution geological mapping based on SLIC-CNN[J]. Isprs International Journal of Geo-Information, 2020, 9 (2): 99. |
| [1] | 肖凡, 杨华清, 唐奥, 黄旋财, 王翠翠. 基于机器学习与多源数据融合的东天山戈壁沙漠覆盖区中-酸性侵入岩岩性填图[J]. 地学前缘, 2025, 32(4): 199-212. |
| [2] | 肖克炎, 李程, 唐瑞, 王瑶, 孙莉, 柳炳利, 樊铭静. 大数据智能预测评价[J]. 地学前缘, 2025, 32(4): 20-37. |
| [3] | 陈勇华, 侯卫生, 郭清锋, 杨松桦, 叶舒婉, 李鑫. 地铁沿线地质结构三维随机重建方法研究[J]. 地学前缘, 2025, 32(4): 222-234. |
| [4] | 张雨飞, 张杨, 吉俊杰, 成秋明. 基于机器学习方法的南海洋壳大地热流预测[J]. 地学前缘, 2025, 32(4): 235-249. |
| [5] | 简富源, 张子鸣, 董岳霖, 张文璟, 郝风云, 王一鸣, 王宇, 张振杰. 基于多重分形与随机森林的新疆哈巴河金矿成矿预测[J]. 地学前缘, 2025, 32(4): 78-94. |
| [6] | 李金明, 张杨, 成秋明. 基于机器学习与垂向分层建模联合驱动的华北克拉通地温梯度空间分布预测[J]. 地学前缘, 2025, 32(4): 291-302. |
| [7] | 李凤磊, 林承焰, 王蛟, 任丽华, 张国印, 朱永峰, 李世银, 张银涛, 关宝珠. 超深层断缝带岩溶缝洞体储层结构分析与智能预测[J]. 地学前缘, 2025, 32(2): 311-331. |
| [8] | 褚宴佳, 何宝南, 陈珍, 何江涛. 基于随机森林模型识别浅层地下水TDS异常的方法研究[J]. 地学前缘, 2025, 32(2): 456-468. |
| [9] | 张必敏, 王学求, 周建, 王玮, 刘汉粮, 刘东盛, Sounthone LAOLO, Phomsylalai SOUKSAN, 谢淼, 董春放, 柳青青, 鲁岳鑫, 王浩楠, 贺彬. 老挝铜资源成矿规律与基于机器学习的远景预测[J]. 地学前缘, 2025, 32(1): 61-77. |
| [10] | 董少群, 曾联波, 冀春秋, 张延兵, 郝静茹, 徐小童, 韩高松, 徐辉, 李海明, 李心琦. 超深层致密砂岩裂缝测井识别深度核方法[J]. 地学前缘, 2024, 31(5): 166-176. |
| [11] | 周永章, 肖凡. 管窥人工智能与大数据地球科学研究新进展[J]. 地学前缘, 2024, 31(4): 1-6. |
| [12] | 万成舟, 季晓慧, 杨眉, 何明跃, 张招崇, 曾姗, 王玉柱. 基于渐进多粒度训练深度学习的矿物图像识别[J]. 地学前缘, 2024, 31(4): 112-118. |
| [13] | 张焕宝, 贺海洋, 杨仕教, 李亚林, 毕文军, 韩世礼, 郭钦鹏, 杜青. 基于机器学习的埃达克质岩构造背景判别研究[J]. 地学前缘, 2024, 31(4): 417-428. |
| [14] | 谷浩, 杨泽强, 高猛, 唐相伟, 王东晓, 刘奎松, 杨树人, 郭跃闪, 王云, 王功文. 河南围山城金银矿集区三维地质建模与成矿预测[J]. 地学前缘, 2024, 31(3): 245-259. |
| [15] | 廖舟, 李梅. 基于开源GemPy的城市地下空间三维隐式势场建模方法研究[J]. 地学前缘, 2024, 31(3): 482-497. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||