地热能可持续开发利用的数值模拟软件OpenGeoSys:原理与应用

doi:10.13745/j.esf.2020.1.18

地学前缘 ›› 2020, Vol. 27 ›› Issue (1): 170-177.DOI: 10.13745/j.esf.2020.1.18

• 地热开发利用模拟和实践 • 上一篇下一篇

地热能可持续开发利用的数值模拟软件OpenGeoSys:原理与应用

孔彦龙¹^,²^,³(), 黄永辉¹^,², 郑天元⁴, 陆仁超⁵, 潘晟¹^,²^,³, 邵亥冰⁵, 庞忠和¹^,²^,³

1.中国科学院地质与地球物理研究所; 中国科学院页岩气与地质工程重点实验室, 北京 100029
2.中国科学院地球科学研究院, 北京 100029
3.中国科学院大学, 北京 100049
4.中国海洋大学, 山东青岛 266100
5.德国亥姆霍兹环境研究中心, 萨克森州莱比锡 04318

收稿日期:2019-03-31 修回日期:2019-12-30 出版日期:2020-01-20 发布日期:2020-01-20
作者简介:孔彦龙(1987—),男,副研究员,主要从事示踪水文地质与热储工程研究。E-mail: ylkong@mail.iggcas.ac.cn
基金资助:
国家重点研发计划项目(2018YFB1501801)

Principle and application of OpenGeoSys for geothermal energy sustainable utilization

KONG Yanlong¹^,²^,³(), HUANG Yonghui¹^,², ZHENG Tianyuan⁴, LU Renchao⁵, PAN Sheng¹^,²^,³, SHAO Haibing⁵, PANG Zhonghe¹^,²^,³

1. Institute of Geology and Geophysics, Chinese Academy of Sciences; Key Laboratory of Shale Gas and Geoengineering, Chinese Academy of Science, Beijing 100029, China
2. Institutions of Earth Science, Chinese Academy of Sciences, Beijing 100029, China
3. University of Chinese Academy of Sciences, Beijing 100049, China
4. Ocean University of China, Qingdao 266100, China
5. Helmholtz Centre for Environmental Research-UFZ, Leipzig 04318, Germany

Received:2019-03-31 Revised:2019-12-30 Online:2020-01-20 Published:2020-01-20

摘要/Abstract

摘要：

地热能规模化利用的可持续开发,通常需要建立数学模型,以实现定量管理和预测。文章评述OpenGeoSys(OGS)数值模拟软件及其在地热资源开发利用过程中的应用算例。OGS是一款基于有限元的免费开源软件,它可处理与地热能开发相关的水流场-温度场-力学场-化学场等多场耦合过程。OGS已应用在国内外多个地热场地,文中着重介绍它在浅层地热能的流体温度变化预测、水热型地热能开发过程中的采灌井距优化、结垢机理和干热岩开发过程中的渗透性演化等方面的应用算例,为地热能的开发提供计算手段和参考。

关键词: OpenGeoSys, 多场耦合, 地热能, 数值模拟

Abstract:

Numerical simulation is very useful in utilizing large scale geothermal energy, predicting reservoir response and optimizing exploitation procedure. Here we describe the OpenGeoSys (OGS) software used to simulate the complex processes in geoscience and hydrological applications, focusing on its application in geothermal energy utilization. OGS is based on an object-oriented finite element method concept and can deal with numerical simulation of thermo-hydro-mechanical-chemical processes in porous media. Case studies related to shallow geothermal energy (temperature and pressure prediction), hydrothermal energy (optimization on the distance between production well and reinjection well, scaling) and hot dry rock (hydraulic fracturing, permeability evolution) are shown with the purpose to help managing geothermal energy utilization.

Key words: OGS, multi-fields coupling, geothermal energy, numerical simulation

中图分类号:

P314

孔彦龙, 黄永辉, 郑天元, 陆仁超, 潘晟, 邵亥冰, 庞忠和. 地热能可持续开发利用的数值模拟软件OpenGeoSys:原理与应用[J]. 地学前缘, 2020, 27(1): 170-177.

KONG Yanlong, HUANG Yonghui, ZHENG Tianyuan, LU Renchao, PAN Sheng, SHAO Haibing, PANG Zhonghe. Principle and application of OpenGeoSys for geothermal energy sustainable utilization[J]. Earth Science Frontiers, 2020, 27(1): 170-177.

图/表 14

图1 OGS中水流场-温度场-力学场-化学场等的耦合原理(据文献[4]修改)

Fig.1 The coupling of thermo-hydro-mechanical-chemical processes by OGS. Modified after [4].

表1 OGS多场耦合公式中的符号变量注释表

Table 1 Parameters in the coupling equations of OGS

量符号	量名称及单位	量符号	量名称及单位
$n →$	外边界的外法线方向单位矢量	Γ_n	Neumann边界条件
$с$	流体比热/(J·m^-3·K^-1)	q^к	源汇项
$ρ$	流体密度/(kg·m^-3)	$Ф$	孔隙度
T	流体温度/℃	ρ_β	β相的密度/(kg·m^-3)
K	岩石导热系数/(W·m^-1·K^-1)	S_β	β相的饱和度
q	热源/(W·m^-2)	$X β к$	组分к在β相中的质量分数
h_β	β相的热焓	$κ →$	绝对渗透率张量
$σ →$	应力张量	κ_rβ	β相的相对渗透率
$g →$	重力加速度/(m·s^-2)	μ_β	β相的黏度/(Pa·s)
$σ$	主应力/Pa	P_β	β相的压力/Pa
S^l	液相饱和度	$D → β к$	组分к在β相中扩散系数
S^ɡ	气相饱和度	G°_p_,_T	定温压下系统吉布斯函数变化
p^l	液相压强/Pa	R	理想气体常数
p^ɡ	气相压强/Pa	$K p, T$	定温压下的化学平衡常数
I	单位矩阵	$a w, a m$	活度
$β T$	热膨胀系数	$γ i, γ j$	逸度系数
V_n	体积/m³	C_i,C_j	热容
M^к	质量矩阵	$v wj, v ij, v mj, v ɡ j$	反应方程式中的化学计量数
$F → β$ , $F → к$ , $F → β к$	达西流量	$f ɡ$	逸度

表1 OGS多场耦合公式中的符号变量注释表

Table 1 Parameters in the coupling equations of OGS

量符号	量名称及单位	量符号	量名称及单位
$n →$	外边界的外法线方向单位矢量	Γ_n	Neumann边界条件
$с$	流体比热/(J·m^-3·K^-1)	q^к	源汇项
$ρ$	流体密度/(kg·m^-3)	$Ф$	孔隙度
T	流体温度/℃	ρ_β	β相的密度/(kg·m^-3)
K	岩石导热系数/(W·m^-1·K^-1)	S_β	β相的饱和度
q	热源/(W·m^-2)	$X β к$	组分к在β相中的质量分数
h_β	β相的热焓	$κ →$	绝对渗透率张量
$σ →$	应力张量	κ_rβ	β相的相对渗透率
$g →$	重力加速度/(m·s^-2)	μ_β	β相的黏度/(Pa·s)
$σ$	主应力/Pa	P_β	β相的压力/Pa
S^l	液相饱和度	$D → β к$	组分к在β相中扩散系数
S^ɡ	气相饱和度	G°_p_,_T	定温压下系统吉布斯函数变化
p^l	液相压强/Pa	R	理想气体常数
p^ɡ	气相压强/Pa	$K p, T$	定温压下的化学平衡常数
I	单位矩阵	$a w, a m$	活度
$β T$	热膨胀系数	$γ i, γ j$	逸度系数
V_n	体积/m³	C_i,C_j	热容
M^к	质量矩阵	$v wj, v ij, v mj, v ɡ j$	反应方程式中的化学计量数
$F → β$ , $F → к$ , $F → β к$	达西流量	$f ɡ$	逸度

图2 OGS的使用流程和处理的数据格式(据文献[4]修改)

Fig.2 Flowchart of OGS application and data input requirements. Modified after [4].

图3 OGS地源热泵模块的概念模型

Fig.3 The conceptual model of ground source heat pumps in OGS

图4 OGS平台中地源热泵模块的验证(据文献[8])

Fig.4 Verification of the ground source heat pump module in OGS. Adapted from [8].

图5 OGS平台中热流固耦合模型的验证(据文献[11]) (a)—模型设置; (b)—压力的验证; (c)—位移的验证; (d)—温度的验证。

Fig.5 Verification of the thermo-hydro-mechanical process through point injection test. Adapted from [11].

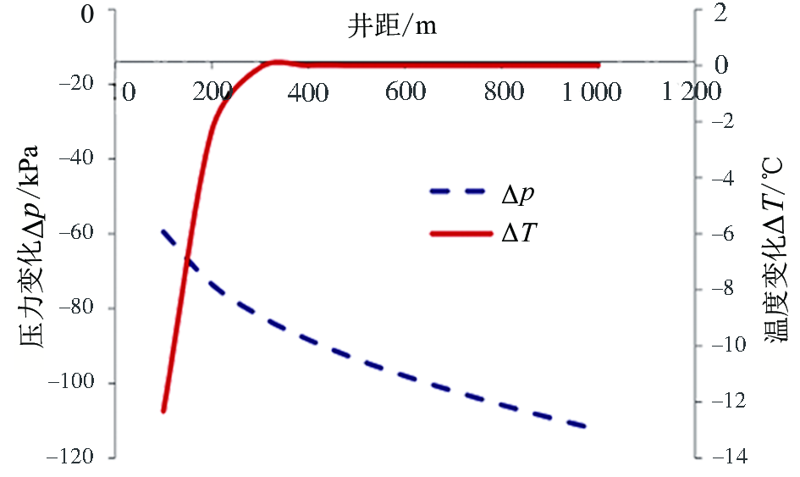
图6 50年后不同采灌井距下的温度与压力变化(据文献[12])

Fig.6 Pressure and temperature change with distance between the production and re-injection wells after 50 years. Adapted from [12].

图7 生产井内管道压力随深度变化曲线

Fig.7 Pressure profile along the production well

图8 溶解态二氧化碳物质的量随深度变化曲线

Fig.8 Change of dissolved carbon dioxide along the production well

图9 OGS模拟深井换热系统长时间运行后的温度变化(据文献[14])

Fig.9 Change of inlet and outlet water temperatures in the deep borehole heat exchanger system after long time operation. Adapted from [14].

图10 定流量的情况下水力压裂过程中地层垂直方向上位移云图

Fig.10 Vertical displacement in hydraulic fracturing under prescribed injected fluid volume

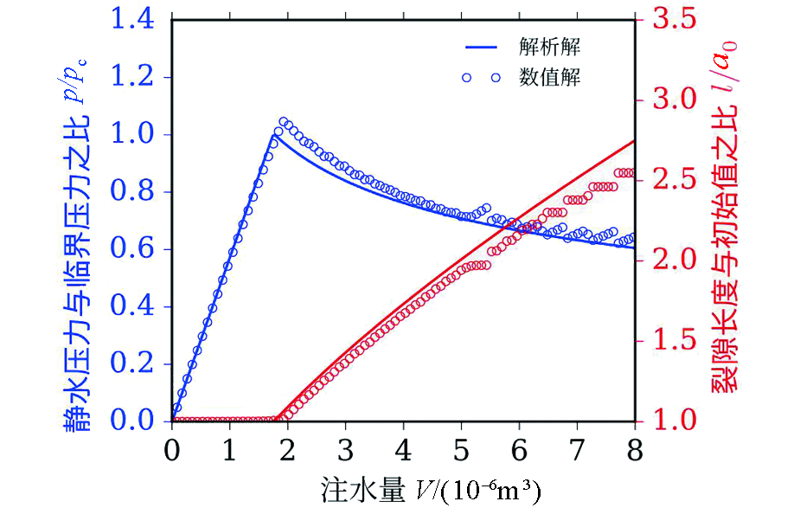
图11 流体压力和开裂长度随注水流量变化曲线(据文献[17])

Fig.11 Comparison between analytical and numerical solutions in terms of hydraulic pressure and crack length vs. injection fluid volume. Adapted from [17].

图12 接触面上加压溶解反应示意图(据文献[19])

Fig.12 Schematic diagram of pressure solution at contact surface. Adapted from [19].

图13 裂隙渗透率随时间变化曲线(据文献[19,20])

Fig.13 Comparison between experimental and simulated results in terms of evolution of hydraulic aperture under varying hydrothermal conditions. Adapted from [19-20].

参考文献 25

[1]	汪集旸, 胡圣标, 庞忠和, 等. 中国大陆干热岩地热资源潜力评估[J]. 科技导报, 2012, 30(32):25-31.
[2]	KONG Y L, PANG Z H, SHAO H B, et al. Recent studies on hydrothermal systems in China: a review[J]. Geothermal Energy, 2014, 2:19. DOI URL
[3]	庞忠和. 地下水运动对地温场的影响: 研究进展综述[J]. 水文地质工程地质, 1987, 14(3):30-34.
[4]	KOLDITZ O, BAUER S, BILKE L, et al. OpenGeoSys: an open-source initiative for numerical simulation of thermo-hydro-mechanical/chemical (THM/C) processes in porous media[J]. Environmental Earth Sciences, 2012, 67(2):589-599. DOI URL
[5]	KOLDITZ O, GÖRKE U J, SHAO H, et al. Thermo-hydro-mechanical/chemical processes in porous media: lecture notes in computational science and engineering[M]. Heidelberg: Springer, 2012: 344.
[6]	KOLDITZ O, SHAO H, WANG W Q, et al. Thermo-hydro-mechanical-chemical processes in fractured porous media: modelling and benchmarking[M]. Heidelberg: Springer, 2016: 217.
[7]	BEIER R A, SMITH M D, SPITLER J D. Reference data sets for vertical borehole ground heat exchanger models and thermal response test analysis[J]. Geothermics, 2011, 40(1):79-85. DOI URL
[8]	ZHENG T Y, SHAO H B, S. SCHELENZ S, et al. Efficiency and economic analysis of utilizing latent heat from groundwater freezing in the context of borehole heat exchanger coupled ground source heat pump systems[J]. Applied Thermal Engineering, 2016, 105:314-326. DOI URL
[9]	EROL S, FRANCOIS B. Freeze damage of grouting materials for borehole heat exchanger: experimental and analytical evaluations[J]. Geomechanics for Energy and the Environment, 2016, 5:29-41. DOI URL
[10]	ESEN H, INALLI M, ESEN Y. Temperature distributions in boreholes of a vertical ground-coupled heat pump system[J]. Renewable Energy, 2009, 34(12):2672-2679. DOI URL
[11]	ZHENG T Y, MIAO X Y, NAUMOV G, et al. A thermo-hydro-mechanical finite element model with freezing and thawing processes in saturated soils for geotechnical engineering[J]. Environmental Geotechnics, 2019, 6:1-13. DOI URL
[12]	KONG Y L, PANG Z H, SHAO H B, et al. Optimization of well-doublet placement in geothermal reservoirs using numerical simulation and economic analysis[J]. Environmental Earth Sciences, 2017, 76(3):118. DOI URL
[13]	AKIN T, GUNEY A, KARGI H. Modeling of calcite scaling and estimation of gas breakout depth in a geothermal well by using PHREEQC [C]//Proceedings of the 40th Workshop on Geothermal Reservoir Engineering. Stanford, California, 2015.
[14]	孔彦龙, 陈超凡, 邵亥冰, 等. 深井换热技术原理及其换热量评估[J]. 地球物理学报, 2017, 60(12):4741-4752.
[15]	TESTER J W, ANDERSON B J, BATCHELOR A S. et al. The future of geothermal energy: impact of Enhanced Geothermal Systems (EGS) on the United States in the 21st Century[M]. Cambridge: Massachusetts Institute of Technology Press, 2006: 358.
[16]	WATANABE N, WANG W, TARON J, et al. Lower-dimensional interface elements with local enrichment: application to coupled hydro-mechanical problems in discretely fractured porous media[J]. International Journal for Numerical Methods in Engineering, 2012, 90(8):1010-1034.
[17]	YOSHIOKA K, PARISIO F, NAUMOV D, et al. Comparative verification of discrete and smeared numerical approaches for the simulation of hydraulic fracturing[J]. International Journal on Geomathematics, 2019, 10(1):13.
[18]	BOND A, BRUSKY I, CHITTENDEN N, et al. Development of approaches for modelling coupled thermal-hydraulic-mechanical-chemical processes in single granite fracture experiments[J]. Environmental Earth Sciences, 2016, 75(19):1313. DOI URL
[19]	LU R C, NAGEL T, SHAO H, et al. Modeling of dissolution-induced permeability evolution of a granite fracture under crustal conditions[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(7):5609-5627. DOI URL
[20]	YASUHARA H, KINOSHITA N, OHFUJI H, et al. Temporal alteration of fracture permeability in granite under hydrothermal conditions and its interpretation by coupled chemo-mechanical model[J]. Applied Geochemistry, 2011, 26(12):2074-2088. DOI URL
[21]	HUANG Y H, KOLDITZ O, SHAO H B. Extending the persistent primary variable algorithm to simulate non-isothermal two-phase two-component flow with phase change phenomena[J]. Geothermal Energy, 2015, 3(1):13. DOI URL
[22]	HUANG Y H, SHAO H B, WIELAND E, et al. A new approach to coupled two-phase reactive transport simulation for long-term degradation of concrete[J]. Construction and Building Materials, 2018, 190:805-829. DOI URL
[23]	NAGEL T, SHAO H, SINGH A K, et al. Non-equilibrium thermochemical heat storage in porous media: Part 1-Conceptual model[J]. Energy, 2013, 60:254-270. DOI URL
[24]	MIAO X Y, KOLDITZ O, NAGEL T. Modelling thermal performance degradation of high and low-temperature solid thermal energy storage due to cracking processes using a phase-field approach[J]. Energy Conversion and Management, 2019, 180:977-989. DOI URL
[25]	YAPPAROVA A, MIRON G D, KULIK D A, et al. An advanced reactive transport simulation scheme for hydrothermal systems modelling[J]. Geothermics, 2019, 78:138-153. DOI URL

地热能可持续开发利用的数值模拟软件OpenGeoSys:原理与应用

Principle and application of OpenGeoSys for geothermal energy sustainable utilization

RichHTML

PDF (PC)

可视化

摘要/Abstract

引用本文

使用本文

图/表 14

参考文献 25

相关文章 15

编辑推荐

Metrics

本文评价

[1]	石鸿蕾, 王婉丽, 王贵玲, 邢林啸, 陆川, 赵佳怡, 刘禄, 宋嘉佳. 典型高温地热系统水热循环及锂同位素分馏过程模拟研究[J]. 地学前缘, 2024, 31(6): 104-119.
[2]	王婉丽, 段雅娟, 张薇, 朱喜, 马峰, 王贵玲. 基于管控单元的城市尺度浅层地热能开发控制因素及指引导则:以雄安新区起步区为例[J]. 地学前缘, 2024, 31(6): 158-172.
[3]	上官拴通, 田兰兰, 潘苗苗, 杨风良, 岳高凡, 苏野, 齐晓飞. 干热岩开发断层滑动及诱发地震风险研究:以唐山马头营干热岩场地为例[J]. 地学前缘, 2024, 31(6): 252-260.
[4]	杨冰, 孟童, 郭华明, 连国玺, 陈帅瑶, 杨曦. 基于K_d的某酸法地浸铀矿山地下水铀运移模拟[J]. 地学前缘, 2024, 31(3): 381-391.
[5]	侯玉松, 胡晓农, 吴吉春. 不同胶结度的多孔介质中溶质横向弥散的孔隙尺度模拟研究[J]. 地学前缘, 2024, 31(3): 59-67.
[6]	刘德民, 王杰, 姜淮, 赵悦, 郭铁鹰, 杨巍然. 青藏高原形成演化动力机制及其远程效应[J]. 地学前缘, 2024, 31(1): 154-169.
[7]	孙焕泉, 毛翔, 吴陈冰洁, 国殿斌, 王海涛, 孙少川, 张英, 罗璐. 地热资源勘探开发技术与发展方向[J]. 地学前缘, 2024, 31(1): 400-411.
[8]	李玉丹, 游瑜春, 曾大乾, 石志良, 顾少华, 张睿. 底水气藏水侵规律数值模拟研究:以元坝长兴组气藏为例[J]. 地学前缘, 2023, 30(6): 341-350.
[9]	张允, 康志江, 马郡伟, 郑欢, 吴大卫. 深层离散裂缝油藏多尺度流固耦合数值模拟方法[J]. 地学前缘, 2023, 30(6): 365-370.
[10]	孙哲, 张彬, 陈大伟, 李玉涛, 王汉勋. 花岗岩裂隙岩体油水两相渗流可视化试验及数值模拟研究[J]. 地学前缘, 2023, 30(3): 465-475.
[11]	何碧竹, 郑孟林, 贠晓瑞, 蔡志慧, 焦存礼, 陈希节, 郑勇, 马绪宣, 刘若涵, 陈辉明, 张盛生, 雷敏, 付国强, 李振宇. 青海共和盆地结构构造与能源资源潜力[J]. 地学前缘, 2023, 30(1): 81-105.
[12]	邢会林, 王建超, 逄硕, 王瑞泽, 刘冬豫, 马子涵, 张愉玲, 谭玉阳. 俯冲带深海-岩石圈流体交换及其效应[J]. 地学前缘, 2022, 29(5): 246-254.
[13]	孙辉, 刘晓东. 青藏高原隆升气候效应的数值模拟研究进展概述[J]. 地学前缘, 2022, 29(5): 300-309.
[14]	熊贵耀, 吴吉春, 杨蕴, 祝晓彬, 刘梦雯, 宋亚霖. 有机污染土壤-地下水系统中的微生物场及多场耦合研究[J]. 地学前缘, 2022, 29(3): 189-199.
[15]	沈晓芳, 万玉玉, 王利刚, 苏小四, 董维红. 基于多相流数值模拟的某石油污染场地地下水中VOCs自然衰减过程识别及能力评估[J]. 地学前缘, 2021, 28(5): 90-103.