

Earth Science Frontiers ›› 2021, Vol. 28 ›› Issue (3): 6-25.DOI: 10.13745/j.esf.sf.2021.1.17
Previous Articles Next Articles
Received:2021-01-18
Revised:2021-02-20
Online:2021-05-20
Published:2021-05-23
CLC Number:
CHENG Qiuming. What are Mathematical Geosciences and its frontiers?[J]. Earth Science Frontiers, 2021, 28(3): 6-25.

Fig.4 (A) Euler geometry applied to plate tectonics; (B) Explanation of the conjugate relationship among the mid-ocean ridge,subduction zone and transformation fault according to Euler vector theorem (adapted from [17]); (C) Map showing the conjugate relationship among mid-ocean ridge,subduction zone and transform faults in the Pacific and North America subduction zones

Fig.8 Application of the spectral energy density-area (S-A) method to Zn anomaly and related background analyses in the Lanping-Jinding district in Yunnan Province

Fig.9 Fractal geometry, density and mechanism. (A) Concepts of fractal density; (B) Possible geological processes that may generate fractal density; (C) Mechanisms of fractal density generation.
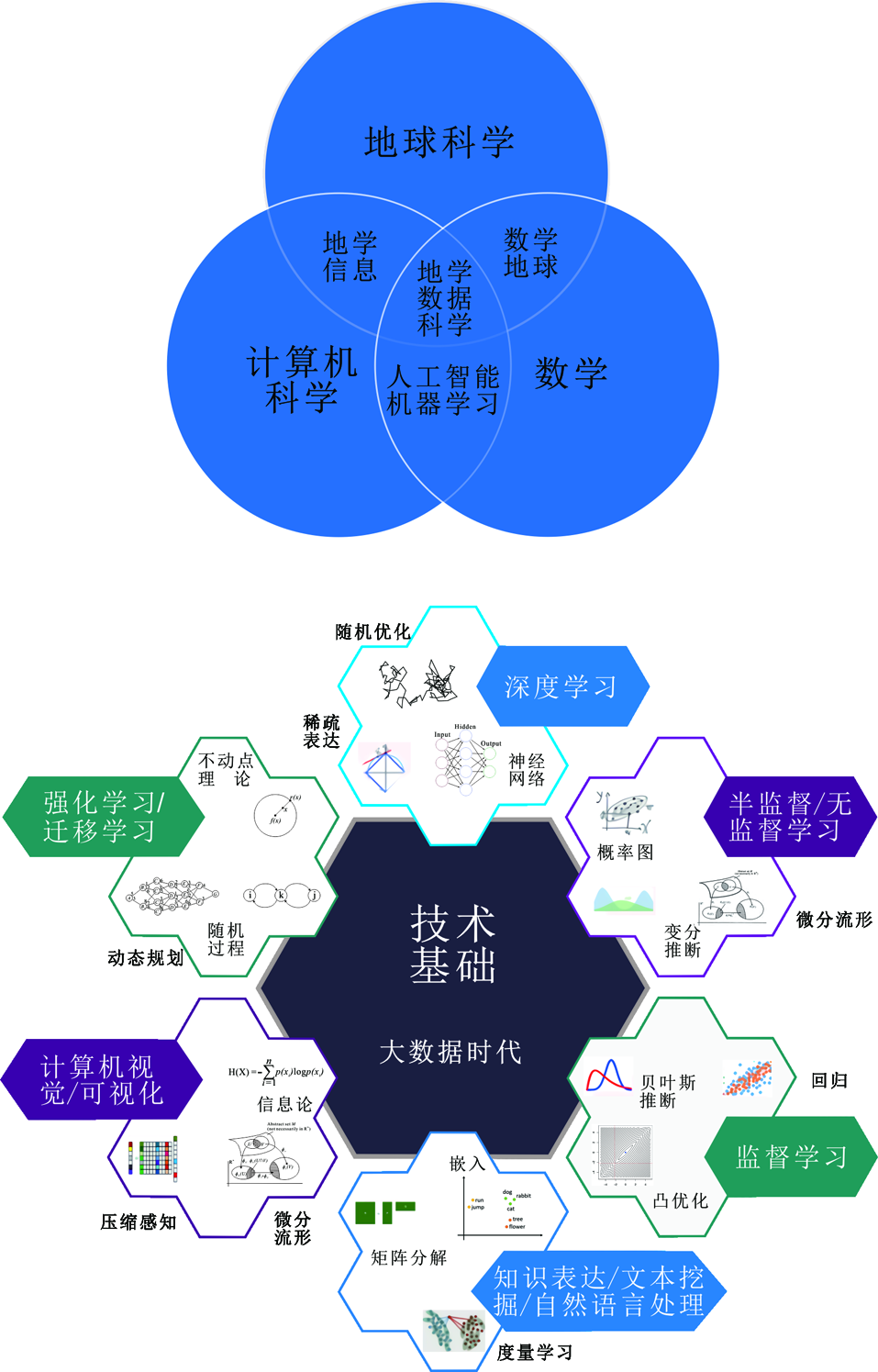
Fig.10 Interdisciplinary relationships of various natural science fields related to geo-data science (upper diagram), and the realm of machine learning where various mathematical subjects support its development
| [1] | HOWARTH R J. Dictionary of mathematical geosciences: with historical notes[M]. Cham, Switzerland: Springer, 2017. |
| [2] |
CHENG Q M. Generalized binomial multiplicative cascade processes and asymmetrical multifractal distributions[J]. Nonlinear Processes in Geophysics, 2014, 21(2):477-487.
DOI URL |
| [3] | CHENG Q M. Mathematical geosciences: local singularity analysis of nonlinear earth processes and extreme geo-events[M]// DAYA SAGAR B S, CHENG Q M, AGTERBERG F P. Handbook of Mathematical Geosciences. Cham, Switzerland: Springer, 2018. |
| [4] | VISTELIUS A B. Problems of mathematical geology: a contribution to the history of the problem[J]. Geologiya i Geofizika, 1962, 12(7):3-9. |
| [5] | MCCAMMON R B. Concepts in geostatistics[M]. Cham, Switzerland: Springer, 1975. |
| [6] | MERRIAM D F. Geostatistics. computer applications in the Earth sciences[M]. Boston, MA: Springer, 1970. |
| [7] | AGTERBERG F P. Geomathematics, mathematical background and geo-science application[M]. Amsterdam: Elsevier, 1974. |
| [8] | AGTERBERG F P. Geomathematics: theoretical foundations, applications and future developments[M]. Cham, Switzerland: Springer, 2014. |
| [9] | KRIGE D G. A statistical approach to some basic mine valuation problems on the Witwatersrand[J]. Journal of the Southern African Institute of Mining Metallurgy, 1951, 52(6):119-139. |
| [10] | MATHERON G. Traité de géostatistique appliquée[M]. Paris: Editions Technip, 1962. |
| [11] |
DIMITRAKOPOULOS R, MUSTAPHA H, GLOAGUEN E. High-order statistics of spatial random fields: exploring spatial cumulants for modeling complex non-gaussian and non-linear phenomena[J]. Mathematical Geosciences, 2010, 42(1):65-99.
DOI URL |
| [12] | GUARDIANO F B, SRIVASTAVA R M. Multivariate geostatistics: beyond bivariate moments[M]// SOARES A O. Geostatistics Troia’92. Dordrecht: Springer, 1993. |
| [13] |
JOURNEL A, ZHANG T F. The necessity of a multiple-point prior model[J]. Mathematical Geology, 2006, 38(5):591-610.
DOI URL |
| [14] | MARIETHOZ G, CAERS J. Multiple-point geostatistics: stochastic modeling with training images[M]. Hoboken: John Wiley & Sons, 2014. |
| [15] |
CHENG Q M. Multifractal interpolation method for spatial data with singularities[J]. Journal of the Southern African Institute of Mining Metallurgy, 2015, 115(3):235-240.
DOI URL |
| [16] | CHENG Q M. A new model for incorporating spatial association and singularity in interpolation of exploratory data[M]// LEUANGTHONG D, DEUTHSCH C V. Geostatistics Banff 2004. Dordrecht: Springer, 2005: 1017-1025. |
| [17] |
MCKENZIE D P, PARKER R L. The North Pacific: an example of tectonics on a sphere[J]. Nature, 1967, 216(5122):1276-1280.
DOI URL |
| [18] |
MCKENZIE D P. Some remarks on heat flow and gravity anomalies[J]. Journal of Geophysical Research, 1967, 72(24):6261-6273.
DOI URL |
| [19] | HESS H H. The evolution of ocean basins[R]. Princeton: Department of Geology, Princeton University, 1960. |
| [20] |
CHENG Q M. Fractal density and singularity analysis of heat flow over ocean ridges[J]. Scientific Reports, 2016, 6(1):19167.
DOI URL |
| [21] | WEISS C S. über die theorie des epidotsystems[J]. Abhandlungen der Königlichen Akademie der Wissenschaften zu Berlin, 1820:242-269. |
| [22] | BRADLEY C, CRACKNELL A. The mathematical theory of symmetry in solids: representation theory for point groups and space groups[M]. Oxford: Oxford University Press, 2009. |
| [23] | UDDEN J A. The mechanical composition of wind deposits[M]. Lindsborg: Lutheran Augustana Book Concern, 1898. |
| [24] |
WENTWORTH C K. A scale of grade and class terms for clastic sediments[J]. The Journal of Geology, 1922, 30(5):377-392.
DOI URL |
| [25] | KRUMBEIN W C. Size frequency distributions of sediments[J]. Journal of Sedimentary Research, 1934, 4(2):65-77. |
| [26] | RICHESON D S. Euler’s Gem: the polyhedron formula and the birth of topology[M]. Princeton: Princeton University Press, 2008. |
| [27] | TOMLINSON R F. Thinking about GIS: geographic information system planning for managers[M]. RedLands, USA: ESRI, Inc., 2007. |
| [28] | CLARKE F W. The data of geochemistry[M]. Washington DC: US Government Printing Office, 1920. |
| [29] | MASON B H. Victor Moritz Goldschmidt: father of modern geochemistry[M]. Washington DC: Geochemical Society, 1992. |
| [30] |
AHRENS L. A fundamental law of geochemistry[J]. Nature, 1953, 172(4390):1148-1148.
DOI URL |
| [31] |
AUBREY K. Frequency distribution of the concentrations of elements in rocks[J]. Nature, 1954, 174(4420):141-142.
DOI URL |
| [32] |
CHENG Q M, AGTERBERG F, BALLANTYNE S. The separation of geochemical anomalies from background by fractal methods[J]. Journal of Geochemical Exploration, 1994, 51(2):109-130.
DOI URL |
| [33] |
CHENG Q M. Multifractal imaging filtering and decomposition methods in space, Fourier frequency, and eigen domains[J]. Nonlinear Processes in Geophysics, 2007, 14(3):293-303.
DOI URL |
| [34] | SINGER D, MENZIE W D. Quantitative mineral resource assessments: an integrated approach[M]. Oxford: Oxford University Press, 2010. |
| [35] |
AGTERBERG F P. Computer programs for mineral exploration[J]. Science, 1989, 245(4913):76-81.
DOI URL |
| [36] | 赵鹏大. 三联式矿产资源定量预测与评价: 数值化矿产预测理论与实践[J]. 地球科学: 中国地质大学学报, 2001, 27(5):139-148. |
| [37] | 赵鹏大. 地质异常理论与矿床预测: 现代矿产资源评价理论与方法[M]. 北京: 地质出版社, 1998. |
| [38] | 王世称, 成秋明, 范继璋. 金矿资源综合信息评价方法[M]. 长春: 吉林科学技术出版社, 1990. |
| [39] |
CHENG Q M. Mapping singularities with stream sediment geochemical data for prediction of undiscovered mineral deposits in Gejiu, Yunnan Province, China[J]. Ore Geology Reviews, 2007, 32(1/2):314-324.
DOI URL |
| [40] |
CHENG Q M. Non-linear theory and power-law models for information integration and mineral resources quantitative assessments[J]. Mathematical Geosciences, 2008, 40(5):503-532.
DOI URL |
| [41] |
GAUTIER D L, BIRD K J, CHARPENTIER R R, et al. Assessment of undiscovered oil and gas in the Arctic[J]. Science, 2009, 324(5931):1175-1179.
DOI URL |
| [42] |
YASUKAWA K, NAKAMURA K, FUJINAGA K, et al. Tracking the spatiotemporal variations of statistically independent components involving enrichment of rare-earth elements in deep-sea sediments[J]. Scientific Reports, 2016, 6(1):29603.
DOI URL |
| [43] |
OROSEI R, LAURO S E, PETTINELLI E, et al. Radar evidence of subglacial liquid water on Mars[J]. Science, 2018, 361(6401):490-493.
DOI URL |
| [44] |
CHENG Q M. Singularity theory and methods for mapping geochemical anomalies caused by buried sources and for predicting undiscovered mineral deposits in covered areas[J]. Journal of Geochemical Exploration, 2012, 122:55-70.
DOI URL |
| [45] | CHENG Q M, XU Y G. Geophysical data processing and interpreting and for mineral potential mapping in GIS environment[C]// Proceedings of the Fourth Annual Conference of the International Association for Mathematical Geology. Napoli, Italy: De Frede Editore, 1998: 394-399. |
| [46] |
CHENG Q M, XU Y G, GRUNSKY E. Integrated spatial and spectrum method for geochemical anomaly separation[J]. Natural Resources Research, 2000, 9(1):43-52.
DOI URL |
| [47] | 李文昌, 李丽辉, 尹光候. 西南三江南段地球化学数据不同方法处理及应用效果[J]. 矿床地质, 2006, 25(4):501-510. |
| [48] | CARRANZA E J M. Geochemical anomaly and mineral prospectivity mapping in GIS[M]. Amsterdam: Elsevier, 2009. |
| [49] | LAMBERT I, DURRHEIM R, GODOY M, et al. Resourcing future generations: a proposed new IUGS initiative[J]. Episodes: journal of international geosciences, 2013, 36(2):82-86. |
| [50] |
CHENG Q M, OBERHÄNSLI R, ZHAO M. A new international initiative for facilitating data-driven Earth science transformation[J]. Geological Society, London, Special Publications, 2020, 499(1):225-240.
DOI URL |
| [51] | MEDICINE G. A Vision for NSF Earth Sciences 2020—2030: Earth in Time[M]. Washington DC: The National Academies Press, 2020. |
| [52] | SURVEY U S G. U. S. Geological survey 21st-century science strategy 2020-2030[R]. Reston: U.S. Geological Survey, 2021. |
| [53] | KOPPERS A A P, COGGON R. Exploring earth by scientific ocean drilling: 2050 science framework[R]. La Jolla: UC San Diego Library Digital Collections, 2020. |
| [54] | TURCOTTE D L. Modeling geocomplexity: “A new kind of science”[J]. Special Papers-Geological Society of America, 2006, 413:39. |
| [55] | WOLFRAM S. A new kind of science: champaign[M]. Champaign: Wolfram Media, 2002. |
| [56] |
LORENZ E N. Deterministic nonperiodic flow[J]. Journal of Atmospheric Sciences, 1963, 20(2):130-141.
DOI URL |
| [57] |
MANDELBROT B B. How long is the coast of Britain? statistical self-similarity and fractional dimension[J]. Science, 1967, 156(3775):636-638.
DOI URL |
| [58] |
VALENTINE G A, ZHANG D X, ROBINSON B A. Modeling complex, nonlinear geological processes[J]. Annual Review of Earth Planetary Sciences, 2002, 30(1):35-64.
DOI URL |
| [59] |
LOVEJOY S, AGTERBERG F, CARSTEANU A, et al. Nonlinear geophysics: why we need it[J]. EOS, Transactions American Geophysical Union, 2009, 90(48):455-456.
DOI URL |
| [60] |
GUTENBERG B, RICHTER C F. Frequency of earthquakes in California[J]. Bulletin of the Seismological Society of America, 1944, 34(4):185-188.
DOI URL |
| [61] |
SORNETTE D, PISARENKO V. Fractal plate tectonics[J]. Geophysical Research Letters, 2003, 30(3):1105.
DOI URL |
| [62] | OUILLON G, CASTAING C, SORNETTE D. Hierarchical geometry of faulting[J]. Journal of Geophysical Research: Solid Earth, 1996, 101(B3):5477-5487. |
| [63] | PELLETIER J D. Statistical self-similarity of magmatism and volcanism[J]. Journal of Geophysical Research: Solid Earth, 1999, 104(B7):15425-15438. |
| [64] |
CANNAVÒ F, NUNNARI G. On a possible unified scaling law for volcanic eruption durations[J]. Scientific Reports, 2016, 6(1):22289.
DOI URL |
| [65] |
AGTERBERG F P. Multifractal modeling of the sizes and grades of giant and supergiant deposits[J]. International Geology Review, 1995, 37(1):1-8.
DOI URL |
| [66] | MANDELBROT B B. Fractals: form, chance and dimension[M]. San Francisco: W. H. Freeman & Company, 1977. |
| [67] |
MANDELBROT B B. Multifractal measures, especially for the geophysicist[J]. Pure and Applied Geophysics, 1989, 131(1/2):5-42.
DOI URL |
| [68] |
LOVEJOY W S. A survey of algorithmic methods for partially observed Markov decision processes[J]. Annals of Operations Research, 1991, 28(1):47-65.
DOI URL |
| [69] | 成秋明. 成矿过程奇异性与矿产预测定量化的新理论与新方法[J]. 地学前缘, 2007, 14(5):42-53. |
| [70] |
CHENG Q M. Extrapolations of secular trends in magmatic intensity and mantle cooling: implications for future evolution of plate tectonics[J]. Gondwana Research, 2018, 63:268-273.
DOI URL |
| [71] |
CHENG Q M, SUN H Y. Variation of singularity of earthquake-size distribution with respect to tectonic regime[J]. Geoscience Frontiers, 2018, 9(2):453-458.
DOI URL |
| [72] |
CHENG Q M. Singularity analysis of magmatic flare-ups caused by India-Asia collisions[J]. Journal of Geochemical Exploration, 2018, 189:25-31.
DOI URL |
| [73] | TURING A M. Computing machinery and intelligence[J]. Mind, 1950, 59:433-460. |
| [74] |
SAMUEL A L. Some studies in machine learning using the game of checkers[J]. IBM Journal of Research Development, 1959, 3(3):210-229.
DOI URL |
| [75] |
SILVER D, HUANG A, MADDISON C J, et al. Mastering the game of go with deep neural networks and tree search[J]. Nature, 2016, 529(7587):484-489.
DOI URL |
| [76] | BONHAM-CARTER G F. Geographic information systems for geoscientists-modeling with GIS[J]. Computer Methods in the Geoscientists, 1994, 13:398. |
| [77] | CHENG Q M. Application of a newly developed boost Weights of Evidence model(BoostWofE) for mineral resources quantitative assessments[J]. Journal of Jilin University, 2012, 42(6):1976-1985. |
| [78] |
CHENG Q M. BoostWofE: a new sequential weights of evidence model reducing the effect of conditional dependency[J]. Mathematical Geosciences, 2015, 47(5):591-621.
DOI URL |
| [79] |
JOURNEL A G. Combining knowledge from diverse sources: an alternative to traditional data independence hypotheses[J]. Mathematical Geology, 2002, 34(5):573-596.
DOI URL |
| [80] | ZHANG S Y, CHENG Q M, ZHANG S P, et al. Weighted weights of evidence and stepwise weights of evidence and their applications in Sn-Cu mineral potential mapping in Gejiu, Yunnan Province, China[J]. Journal of China University of Geosciences, 2009, 34:281-286. |
| [81] |
AGTERBERG F P. A modified weights-of-evidence method for regional mineral resource estimation[J]. Natural Resources Research, 2011, 20(2):95-101.
DOI URL |
| [82] | LU Z, PU H M, WANG F C, et al. The expressive power of neural networks: a view from the width[J]. ArXiv Preprint, 2017: 1709. 02540. |
| [83] |
ZHAI A R, JIANG J H. Dependence of US hurricane economic loss on maximum wind speed and storm size[J]. Environmental Research Letters, 2014, 9(6):064019.
DOI URL |
| [1] | ZHAO Yu, CHENG Li, YANG Liying, LI Li, XIANG Peng. Earth Science Frontiers: Journal influence assessment based on bibliometric analysis [J]. Earth Science Frontiers, 2024, 31(1): 535-549. |
| [2] | ZHAO Pengda, CHEN Yongqing. Digital geology and quantitative mineral exploration [J]. Earth Science Frontiers, 2021, 28(3): 1-5. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||
