

地学前缘 ›› 2026, Vol. 33 ›› Issue (1): 432-443.DOI: 10.13745/j.esf.sf.2025.10.25
胡立堂1,2( ), 甘霖1,2, 孙建冲1,2,3, 刘宏博1,2, 田蕾1,2, 沈琦1,2
), 甘霖1,2, 孙建冲1,2,3, 刘宏博1,2, 田蕾1,2, 沈琦1,2
收稿日期:2025-08-30
修回日期:2025-10-20
出版日期:2026-11-25
发布日期:2025-11-10
作者简介:胡立堂(1976—),男,教授,博士生导师,主要从事渗流模拟研究。E-mail:litanghu@bnu.edu.cn
基金资助:
HU Litang1,2( ), GAN Lin1,2, SUN Jianchong1,2,3, LIU Hongbo1,2, TIAN Lei1,2, SHEN Qi1,2
), GAN Lin1,2, SUN Jianchong1,2,3, LIU Hongbo1,2, TIAN Lei1,2, SHEN Qi1,2
Received:2025-08-30
Revised:2025-10-20
Online:2026-11-25
Published:2025-11-10
摘要: 模型结构和参数取值的不确定性是制约地下水模型仿真精度和实现高精度管理应用的关键因素。针对这一问题,本文提出了一种基于观测井观测数据的地下水水头模拟误差补偿校正方法。该方法首先对观测井的模拟水位进行误差校正,再利用反距离插值技术估计误差的空间分布,最后将误差补偿应用于模型中其他网格点,实现整体模拟精度的提升。研究基于自主研发的地下水流数值模拟软件,设计了三种真实非均质介质、定流量和变流量抽注水、不同开采井和观测井数量组合的多种模拟情景,系统评估了均质水文地质模型误差补偿校正方法对水头模拟的效果。结果表明,误差补偿校正后的观测井水头模拟精度显著提高,且精度提升程度与渗透系数的平均值成反比、与其方差成正比。在多井抽水注水及强非均质变流量条件下,均方根误差由1.5 m降至0.25 m。通过对多种校正点数量情景的比较分析发现,所提出的方法在校正点位置的模拟效果显著提升,但对空间范围内地下水水头的整体模拟效果提升较为有限。研究方法可提升已识别地下水数值模型的模拟精度,具有较好的推广应用价值。
中图分类号:
胡立堂, 甘霖, 孙建冲, 刘宏博, 田蕾, 沈琦. 考虑参数不确定性的地下水数值模型误差补偿校正方法[J]. 地学前缘, 2026, 33(1): 432-443.
HU Litang, GAN Lin, SUN Jianchong, LIU Hongbo, TIAN Lei, SHEN Qi. Error correction method for groundwater numerical models considering parameter uncertainty[J]. Earth Science Frontiers, 2026, 33(1): 432-443.
| 序号 | 名称 | 统计值 | 真实介质条件 | 概念模型介质条件 | ||
|---|---|---|---|---|---|---|
| 1 | 中等非均质 | 平均值(m/d) | 0.5 | 模型模拟值作为 观测值 | 0.5 | 模型模拟值将 用于校正前、 校正后比较 |
| 方差(m2/d2) | 1.0 | 0.0 | ||||
| 2 | 强非均质 | 平均值(m/d) | 0.5 | 0.5 | ||
| 方差(m2/d2) | 2.0 | 0.0 | ||||
| 3 | 弱非均质 | 平均值(m/d) | 5.0 | 5.0 | ||
| 方差(m2/d2) | 0.5 | 0.0 | ||||
表1 真实与模型概化的渗透系数统计表
Table 1 Statistical parameters of hydraulic conductivities for real sites and model conceptualization
| 序号 | 名称 | 统计值 | 真实介质条件 | 概念模型介质条件 | ||
|---|---|---|---|---|---|---|
| 1 | 中等非均质 | 平均值(m/d) | 0.5 | 模型模拟值作为 观测值 | 0.5 | 模型模拟值将 用于校正前、 校正后比较 |
| 方差(m2/d2) | 1.0 | 0.0 | ||||
| 2 | 强非均质 | 平均值(m/d) | 0.5 | 0.5 | ||
| 方差(m2/d2) | 2.0 | 0.0 | ||||
| 3 | 弱非均质 | 平均值(m/d) | 5.0 | 5.0 | ||
| 方差(m2/d2) | 0.5 | 0.0 | ||||
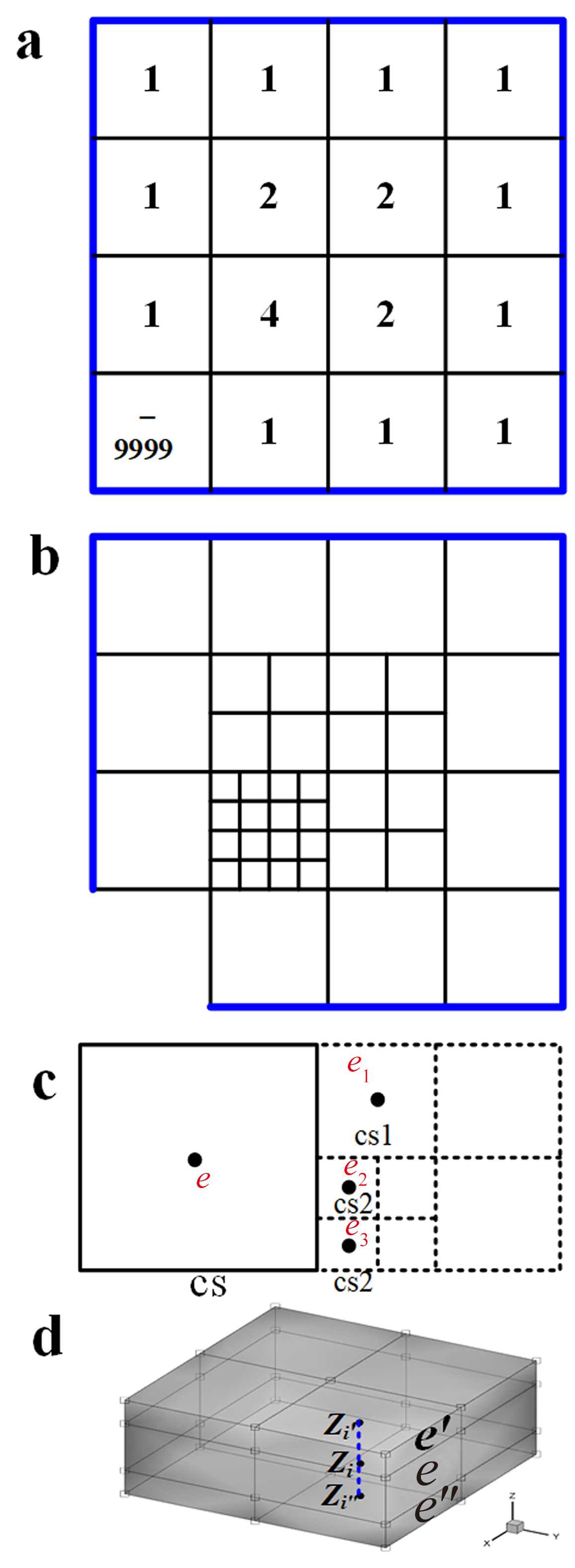
图2 地下水数值模型网格代码(a)、网格划分(b)、平面(c)和垂向(d)水均衡计算示意图
Fig.2 Schematic figures of grid code (a), grid discretization (b),plan view (c), and vertical water balance calculation (d) in groundwater numerical model

图3 校正前(a)、校正后(b)的地下水水头模拟与观测值散点密度图
Fig.3 Scatter-density distributions between simulated and observed hydraulic heads before (a) and after calibration (b)

图4 校正前后典型观测井O1(a)、O2(b)、O3(c)和O4(d)地下水水头变化曲线
Fig.4 Hydraulic head variation curves of typical observation wells O1 (a), O2 (b), O3 (c), and O4 (d) before and after correction
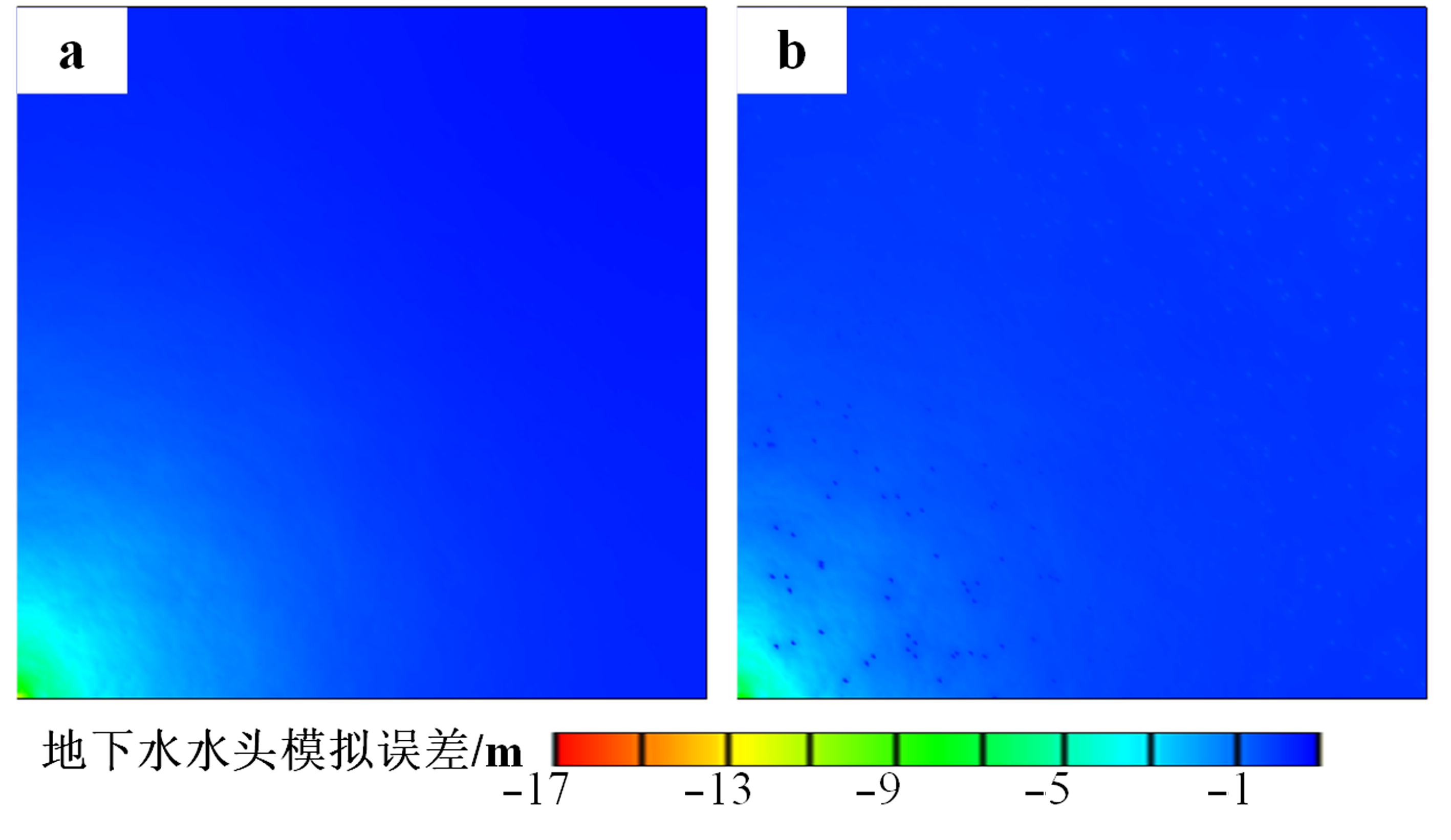
图5 校正前(a)和校正后(b)第2天地下水水头模拟误差空间分布对比
Fig.5 Comparison of the spatial distribution of hydraulic head simulation errors on the 2nd day before (a) and after (b) calibration

图6 强非均质(a)和弱非均质(b)条件下渗透系数对数值的空间分布
Fig.6 Spatial distribution of the logarithm of hydraulic conductivities under strong (a) and weak (b) heterogeneity conditions
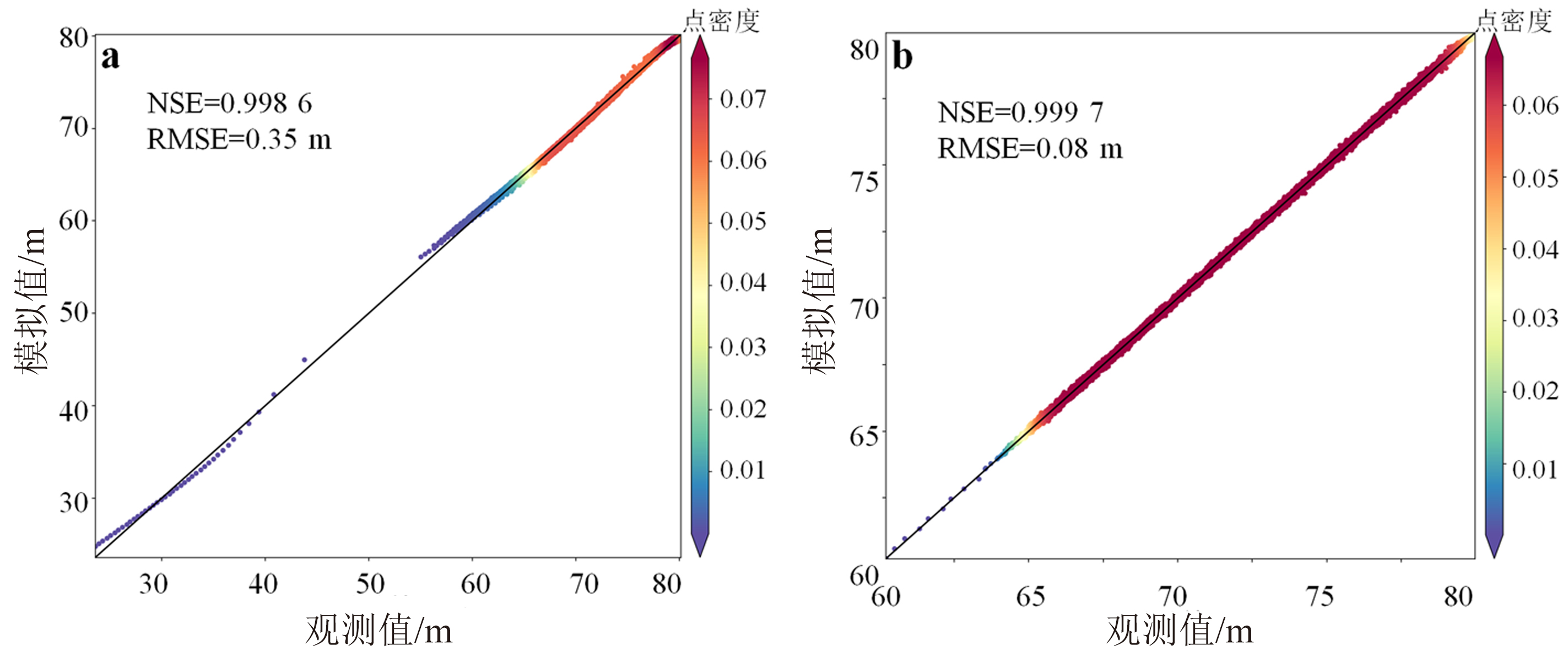
图7 强非均质(a)和弱非均质(b)条件下误差校正后的模拟水头值与观测值散点密度图
Fig.7 Scatter-density distributions between simulated and observed hydraulic head values after error correction under strong (a) and weak (b) heterogeneity conditions

图8 强非均质(a)和弱非均质(b)条件下误差校正后的模拟地下水水头误差分布图
Fig.8 Error distribution maps of simulated hydraulic head after error correction under strong (a) and weak (b) heterogeneity conditions

图9 变流量单井开采时中等非均质(a)、强非均质(b)和弱非均质条件(c)下观测井O1的地下水水头动态变化
Fig.9 Changes of hydraulic head at observation well O1 under moderate (a), strong (b), and weak (c) heterogeneity conditions during variable-rate single-well pumping

图10 不同非均质变流量多井抽注条件下地下水水头和误差值空间分布图:中等非均质条件地下水水头真值(a)、校正前的误差(b)和校正后的误差(c);强非均质条件地下水水头真值(d)、校正前的误差(e)和校正后的误差(f);弱非均质条件地下水水头真值(g)、校正前的误差(h)和校正后的误差(i)
Fig.10 Spatial distribution maps of hydraulic head and error values under variable-rate multi-well pumping and injection conditions with different heterogeneity levels: true hydraulic head (a), error before (b) and after (c) correction under moderate heterogeneity, true hydraulic head (d), error before (e) and after (f) correction under strong heterogeneity, true hydraulic head (g), error before (h) and after (i) correction under weak heterogeneity
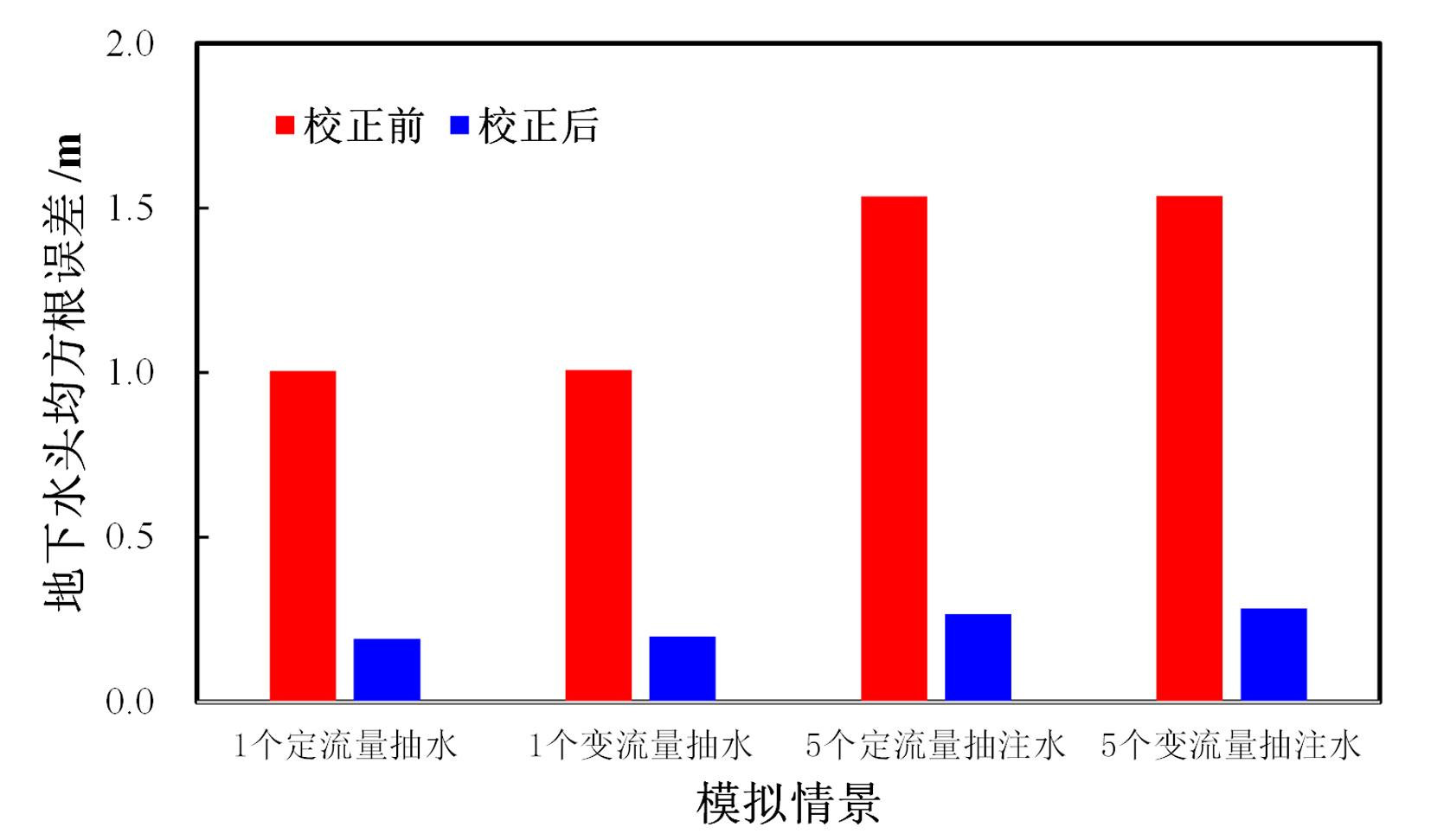
图11 不同抽注条件和强非均质条件地下水水头均方根误差变化
Fig.11 Variation of root mean square error of hydraulic head under strong heterogeneity conditions at different extraction scenarios

图12 强非均质变流量单井开采条件下误差校正前(a)和校正后(b)的模拟水头值与观测值的散点密度图
Fig.12 Scatter-density distributions between simulated and observed hydraulic head values before (a) and after (b) error correction under strong heterogeneity during variable-rate single-well pumping conditions
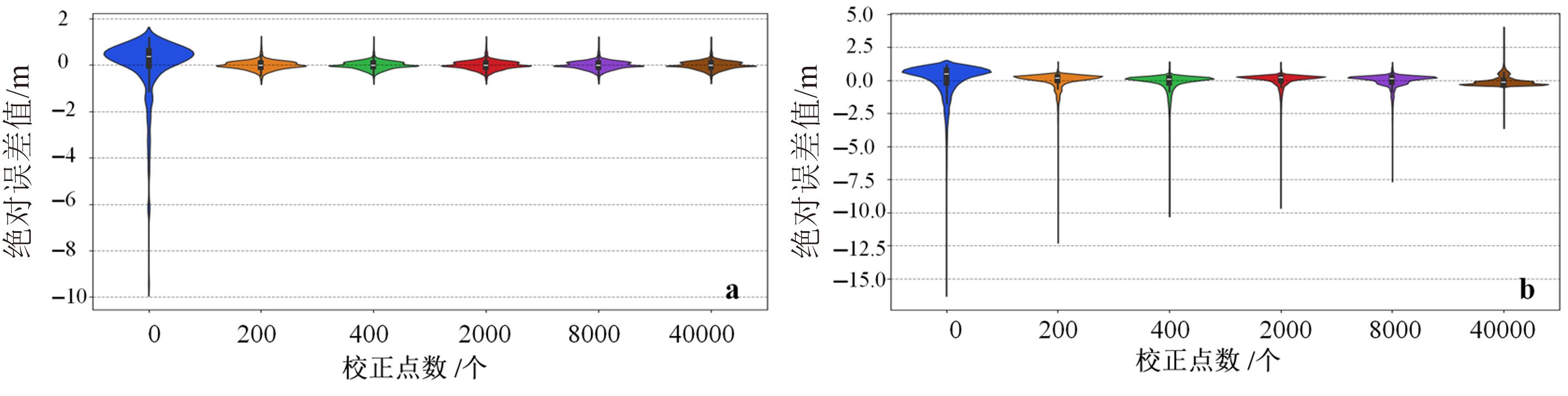
图13 不同校正点数量对观测井地下水水头模拟绝对误差(a)和2天后区域地下水水头绝对误差(b)的对比
Fig.13 Comparison of absolute errors in simulated hydraulic head at observation wells (a) and absolute errors in regional hydraulic head after 2 days (b) under different numbers of calibration points

图14 多井变流量抽注强非均质含水层中观测井O1(a)和O4(b)地下水水头变化曲线
Fig.14 Hydraulic head variation curves for observation wells O1 (a) and O4 (b) simulated by model under multi-well variable flow extraction conditions in strongly heterogeneous media
| [1] |
GORELICK S M, ZHENG C M. Global change and the groundwater management challenge[J]. Water Resources Research, 2015, 51(5): 3031-3051.
DOI URL |
| [2] | 舒乐乐, 陈昊, 孟宪红, 等. 地表-地下过程耦合的数值水文模型综述[J]. 中国科学: 地球科学, 2024, 54(5): 484-1505. |
| [3] | 王浩, 陆垂裕, 秦大庸, 等. 地下水数值计算与应用研究进展综述[J]. 地学前缘, 2010, 17(6): 1-12. |
| [4] |
李洁祥, 许亚东, 蔺文静. 传统水化学地热温度计的适用性分析[J]. 地学前缘, 2024, 31(6): 145-157.
DOI |
| [5] |
弓耀奇, 岳甫均, 刘鑫, 等. 基于流域系统水文水环境耦合模型的氮循环研究进展[J]. 地学前缘, 2025, 32(3): 183-195.
DOI |
| [6] | 陈崇希. “防止模拟失真,提高仿真性”是数值模拟的核心[J]. 水文地质工程地质, 2003, 30(2): 1-5. |
| [7] | CONDON L E, KOLLET S, BIERKENS M, et al. Global groundwater modeling and monitoring: opportunities and challenges[J]. Water Resources Research, 2021, 57(12): e2020WR029500. |
| [8] |
SUN J C, HU L T, LI D D, et al. Data-driven models for accurate groundwater level prediction and their practical significance in groundwater management[J]. Journal of Hydrology, 2022, 608: 127630.
DOI URL |
| [9] | 龚莉, 史浙明, 张宗文, 等. 基于多元分析的某地区垃圾填埋场地下水生态环境风险定量评价[J]. 现代地质, 2024, 38(3): 734-743. |
| [10] | 张天宇, 徐从超, 张钦, 等. 2019—2022年潮白河流域地下水位动态变化及影响因素分析[J]. 现代地质, 2025, 39(4): 1119-1128. |
| [11] |
褚宴佳, 何宝南, 陈珍, 等. 基于随机森林模型识别浅层地下水TDS异常的方法研究[J]. 地学前缘, 2025, 32(2): 456-468.
DOI |
| [12] | VANCE T C, HUANG T, BUTLER K A. Big data in Earth science: emerging practice and promise[J]. Science, 2024, 383(6688): eadh9607. |
| [13] | KUANG X X, LIU J G, SCANLON B R, et al. The changing nature of groundwater in the global water cycle[J]. Science, 2024, 383(6686): f630. |
| [14] |
欧阳恺皋, 蒋小伟, 杜亚楠, 等. 华北“23·7”强降雨事件对不同埋深地下水的补给机理:以雄安新区为例[J]. 地学前缘, 2025, 32(1): 432-439.
DOI |
| [15] |
陈喜, 高满, 董建志, 等. 京津冀地区水资源供需演变面临挑战问题及研究途径[J]. 地学前缘, 2025, 32(3): 436-444.
DOI |
| [16] |
谌宏伟, 朱智超, 李正最, 等. 极端气候下洞庭湖河水-地下水相互作用:以资江洞庭湖河段为例[J]. 地学前缘, 2025, 32(2): 445-455.
DOI |
| [17] |
张学航, 何宝南, 何江涛, 等. 永定河回补区地下水污染风险演化研究[J]. 地学前缘, 2025, 32(4): 523-536.
DOI |
| [18] | 孙玉芳, 金晓媚, 雪彦宏, 等. 宁夏平原鸣翠湖地表水与地下水转化关系[J]. 现代地质, 2024, 38(3): 744-754. |
| [19] | 莫绍星. 基于深度学习的地下水模拟高维不确定性分析和反演[D]. 南京: 南京大学, 2019. |
| [20] |
POETER E. All models are wrong, how do we know which are useful[J]. Groundwater, 2007, 45(4): 390-391.
DOI URL |
| [21] |
GAN L, HU L T, WANG Z J, et al. Decoding the nexus of surface water and groundwater in Northwestern China: insights from long-term irrigation activities and numerical modeling[J]. Journal of Hydrology, 2025, 654: 132825.
DOI URL |
| [22] |
杨轶群, 李燊琰, 戴君一, 等. 滦河口河岸砂质潜水含水层渗透系数尺度效应分析研究[J]. 地学前缘, 2025, 32(3): 425-435.
DOI |
| [23] |
LIU H H. Non-Darcian flow in low-permeability media: key issues related to geological disposal of high-level nuclear waste in shale formations[J]. Hydrogeology Journal, 2014, 22(7):1525-1534.
DOI URL |
| [24] |
HUANG S Q, HU L T, LI B H, et al. Assessing geological structure uncertainties in groundwater models using transition probability-based realizations[J]. Journal of Hydrology, 2025, 651: 132598.
DOI URL |
| [25] |
崔迪, 杨冰, 郭华明, 等. 砂岩含水介质中铀的吸附和迁移行为研究[J]. 地学前缘, 2022, 29(3): 217-226.
DOI |
| [26] |
WANG W C, ZHAO Y W, XU D M, et al. Error correction method based on deep learning for improving the accuracy of conceptual rainfall-runoff model[J]. Journal of Hydrology, 2024, 643: 131992.
DOI URL |
| [27] |
PAN Z D, LU W X, BAI Y K. Groundwater contaminated source estimation based on adaptive correction iterative ensemble smoother with an auto lightgbm surrogate[J]. Journal of Hydrology, 2023, 620: 129502.
DOI URL |
| [28] | SHI W, WAN X, ZHAO F, et al. A dual-model framework combining nonlinear autoregressive with exogenous inputs (NARX) and LSTM networks for enhanced daily runoff prediction and error correction[J]. Environmental Modelling & Software, 2025, 192: 106570. |
| [29] |
SUN J C, HU L T, Cao X Y, et al. A dynamical downscaling method of groundwater storage changes using GRACE data[J]. Journal of Hydrology: Regional Studies, 2023, 50: 101558.
DOI URL |
| [30] |
SUN J C, HU L T, CHEN F, et al. Downscaling simulation of groundwater storage in the Beijing, Tianjin, and Hebei regions of China based on GRACE data[J]. Remote Sensing, 2023, 15: 1490.
DOI URL |
| [31] | JOHNSON R A, WICHERN D W. Applied multivariate statistical analysis[M]. 6th Edition. Upper Saddle River, New Jersey: Pearson Prentice Hall, 2007. |
| [1] | 李胜利, 张亚雄, 于兴河, 付超, 马喜斌. 含煤层系相控型致密气储层非均质性评价的沉积要素与甜点预测策略:以鄂尔多斯盆地为例[J]. 地学前缘, 2025, 32(5): 389-403. |
| [2] | 庞正炼, 陶士振, 张琴, 白斌, 林森虎, 张天舒, 陈燕燕, 范建玮, 孙菲菲. 鄂尔多斯盆地延长组7段夹层型页岩层系石油富集规律与主控因素[J]. 地学前缘, 2023, 30(4): 152-163. |
| [3] | 李玉喜, 何建华, 尹帅, 王濡岳, 代鹏, 赵冬. 页岩油气储层纵向多重非均质性及其对开发的影响[J]. 地学前缘, 2016, 23(2): 118-125. |
| [4] | 王香增,张丽霞,高潮. 鄂尔多斯盆地下寺湾地区延长组页岩气储层非均质性特征[J]. 地学前缘, 2016, 23(1): 134-145. |
| [5] | 刘超,何江涛*,沈杨,刘玉梅,陈鸿汉. 非均质包气带三氮累积转化模拟砂箱试验[J]. 地学前缘, 2012, 19(6): 236-242. |
| [6] | 张章, 朱玉双, 陈朝兵, 牛小兵, 辛红刚, 朱静, 全洪慧. 合水地区长6油层微观渗流特征及驱油效率影响因素研究[J]. 地学前缘, 2012, 19(2): 176-183. |
| [7] | 高兴军, 宋新民, 李淑贞, 孙圆辉, 赵应成, 张为民, 史静, 马文龙. 高含水油田密闭取心检查井水淹状况及主控因素研究:以扶余油田泉四段油层为例[J]. 地学前缘, 2012, 19(2): 162-170. |
| [8] | 王建平, 樊太亮, 王宏语, 刘振兴, 李一凡 , 胡晓兰. 苏德尔特油田铜钵庙组—南屯组油层多级次基准面旋回格架中的储层非均质性特征[J]. 地学前缘, 2012, 19(2): 141-150. |
| [9] | 李胜利, 于兴河, 姜平, 李茂, 李茂文, 晋剑利, 黄国政, 黄月银. 琼东南盆地崖13-1气田陵三段沉积微相对储层非均质性及流动单元划分的影响[J]. 地学前缘, 2010, 17(4): 160-166. |
| [10] | 董书宁, 戴振学, 李竞生. 弥散系数在非均质多相岩层中的尺度效应[J]. 地学前缘, 2010, 17(3): 276-280. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||